Kezdőlap


Feladat:	1333. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Czinczenheim József , Gállik István , Halász Iván , Hörcher János , Komlós János , Krisztonosich Jenő , Nagy Elemér
Füzet:	1937/október, 48. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Parabola egyenlete, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1937/május: 1333. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Koordinátarendszerünk kezdőpontja legyen a kör $O$ középpontja; az $X$ -tengely legyen $e$ -re merőleges. Így a kör, ill. egyenes egyenlete:

\begin{matrix} x^{2} + y^{2} = r^{2} ... & (1) \\ x = a ... & (2) \end{matrix}

ahol

a

O

pontnak az

e

egyenestől való távolsága.
Valamely

(α, β)

pontnak az 1) körre vonatkozó polárisát az

\begin{matrix} α x + β y - r^{2} = 0 \end{matrix}

egyenlet adja meg. Az adott esetben az

A

pontra nézve

α = a

állandó, csak

β

változó; az

A

polárisának egyenlete:

\begin{matrix} a x + β y - r^{2} = 0 ... \end{matrix}

(3)

A

pontban az

e

-re állított merőleges egyenlete:

\begin{matrix} y = β ... \end{matrix}

(4)

A 3) és 4) egyenes

M

metszéspontynak koordinátái kielégítik a 3) és 4) egyenleteket; ha ezekből a változó

β

-t kiküszöböljük, megkapjuk az

M

pont mértani helyének egyenletét:

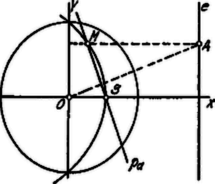\begin{matrix} a x + y^{2} - r^{2} = 0 ill. y^{2} = r^{2} - a x ... \end{matrix}

(5)

Ez oly parabola egyenlete, melynek főtengelye az

X

-tengely (negatív irányban). Csúcsa:

x_{0} = \frac{r^{2}}{a}

abscissához tartozik. Ezen

S

csúcs nem más, mint az e egyenesnek a körre vonatkozó pólusa.
A parabola keresztülmegy az

x = 0

y = \pm r

pontokon, azaz azon pontokon, amelyekben a kör az

Y

-tengelyt metszi.
A parabola gyújtópontja

\frac{a}{4}

távolságban van a csúcstól (a kör középpontja felé).
Minthogy az

A

ponthoz tartozó poláris keresztül megy az

S

ponton és merőleges

O A

-ra, az

S

pont meghatározásával bármely

A

ponthoz tartozó

M

pont könnyen szerkeszthető.

Krisztonosich Jenő (Szent László g. VIII. o. Bp. X.)