Kezdőlap


Feladat:	1332. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Nagy Elemér , Rappaport Sándor
Füzet:	1937/október, 46 - 48. oldal		PDF \| MathML
Témakör(ök):	Negyed- és magasabb fokú függvények, Beírt háromszög, Függvényvizsgálat differenciálszámítással, Egyenlő szárú háromszögek geometriája, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1937/május: 1332. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Független változónak tekintsük az egyenlőszárú háromszög magasságát; ezt jelölje $x$ . Ha $R$ a kör sugara, $0 ≦ x ≦ 2 R$ .
A háromszög alapjának fele: $x$ és $(2 R - x)$ mértani középarányosa és így a háromszög területe

\begin{matrix} y = x \sqrt[]{x (2 R - x)} = \sqrt[]{x^{3} (2 R - x)} . \end{matrix}

Nyilvánvaló, hogy

y

csak akkor valós, ha

0 ≦ x ≦ 2 R

. Elegendő tehát, ha ezen közben az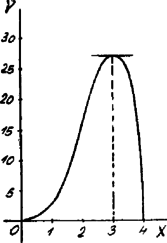

\begin{matrix} f (x) = x^{3} (2 R - x) = - x^{4} + 2 R x^{3} \end{matrix}

függvény változását vizsgáljuk.

f (x) = 0

(és

y = 0

), ha

x = 0

és ha

x = 2 R

. Ezen közben

f (x)

mindenütt folytonos és pozitív; kell tehát, hogy ezen közben legalább egy maximuma legyen. Minthogy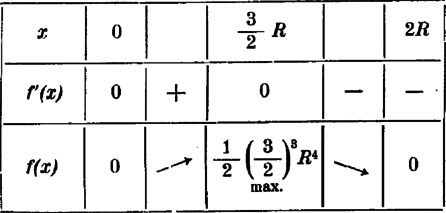

\begin{matrix} f' (x) = - 4 x^{3} + 6 R x^{2} = 2 x^{2} (3 R - 2 x) = 0, \end{matrix}

x = 0

és ha

x = \frac{3 R}{2}

, az

x = \frac{3 R}{2}

helyen

f (x)

függvénynek (és

y

-nak) maximuma van. Ezen helyen

f' (x)

pozitív értékekből negatív értékekbe megy át,

f (x)

változását tehát a következő táblázat jellemzi:

Eszerint

y

ill.

a^{2}

legnagyobb értéke:

\sqrt[]{\frac{1}{2} {(\frac{3}{2})}^{3} R^{4}} = \frac{3 \sqrt[]{3}}{4} R^{2}

. Ez a körbe írt egyenlőoldalú háromszög területe.

y

minden értéket, mely

0

és

\frac{3 \sqrt[]{3}}{4} R^{2}

között van, kétszer vesz fel: egyszer a növekedés, egyszer a csökkenés közben. Ebből következik, hogy ha

a^{2} \leq \frac{3 \sqrt[]{3}}{4} R^{2}

, az

\begin{matrix} x \sqrt[]{x (2 R - x)} = a^{2} ill. x^{3} (2 R - x) = a^{4} \end{matrix}

egyenletnek két valós, pozitív megoldása van.

Kiegészítés. Az

f (x) = x^{3} (2 R - x)

függvénynek az

x = 0

helyen inflexiós pontja van.

f (x) < 0

, ha

x < 0

vagy ha

x > 2 R

. Nyilvánvaló tehát, hogy, mivel

a^{4} > 0

, az

f (x) = a^{4}

egyenletnek nem lehet oly valós megoldása, amely szerint

x < 0

vagy

x > 2 R

.

Az

\begin{matrix} x^{3} (2 R - x) = a^{4} ill. g (x) \equiv x^{4} - 2 R x^{3} + a^{4} = 0 \end{matrix}

egyenletnek a Descartes-féle jelszabály szerint legfeljebb két pozitív gyöke lehet. Ezek egyike

0

és

\frac{3}{2} R

, másik

\frac{3}{2} R

és

2 R

között van, ha

a^{2} < \frac{3 \sqrt[]{3}}{2} R^{2}

.

Ugyanis

\begin{matrix} g (0) = a^{4} > 0, g (\frac{3}{2} R) = {(\frac{3}{2} R)}^{4} - 2 {(\frac{3}{2})}^{3} R^{4} + a^{4} = a^{4} - \frac{1}{2} {(\frac{3}{2})}^{3} R^{4} < 0. \end{matrix}

és

\begin{matrix} g (2 R) = 16 R^{4} - 16 R^{4} + a^{4} > 0. \end{matrix}