Kezdőlap


Feladat:	1320. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Balog Gy. , Bodó Zalán , Cseh Sándor , Fehér György , Gálfi János , Hörcher János , Komlós János , Krisztonosich Jenő , Nagy Elemér , Seidl Gábor , Tésy Gabriella , Vajda József
Füzet:	1937/szeptember, 11 - 13. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Rekurzív eljárások, Mértani sorozat, Síkbeli szimmetrikus alakzatok, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1937/április: 1320. matematika feladat

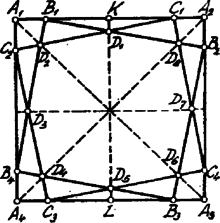
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . Tetszőleges $x$ távolságot mérve fel a jelzett módon a négyzet oldalaira, a $B_{1} B_{2}$ és $C_{1} C_{2}$ távolságok szimmetrikusak a négyzet $K L$ szimmetria tengelyére nézve. $B_{1} B_{4}$ és $C_{2} C_{1}$ pedig az $A_{1} A_{2}$ átlóra nézve s. í. t. Ebből következik,hogy a $D_{1}$ , $D_{3}$ , $D_{5}$ , $D_{7}$ csúcsok a négyzet szembenfekvő oldalait felező szimmetria tengelyeken, a $D_{2}$ , $D_{4}$ , $D_{6}$ , $D_{8}$ csúcsok az átlókon, mint a négyzet szimmetria tengelyein feküsznek.

Másrészt

B_{1} B_{4}

és

C_{1} C_{4}

is szimmetrikus a

K L

-re; ebből következik, hogy

B_{1} D_{1} = C_{1} D_{1}

B_{1} D_{2} = C_{1} D_{8}

és

D_{1} D_{2} = D_{1} D_{8}

s. í. t. ‐ az átlók menti szimmetriát is figyelembe véve ‐ a

D_{1} D_{2} ... D_{8}

összes oldalai egyenlők és^{$^{*}$} csúcsai a négyzet szimmetria-tengelyein feküsznek.

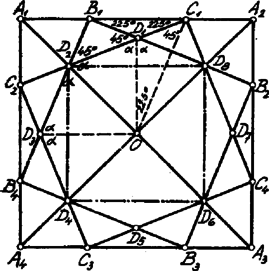
Hogy ezen négyszög szabályos is legyen, szükséges még és elegendő, hogy mindegyik szöge

135^{\circ}

-ú, tehát ábránk szerint

2 α = 135^{\circ} (α = 67, 5^{\circ})

legyen, más szóval: a

D_{1} D_{2} ... D_{8}

nyolcszög oldalai felett fekvő derékszögű háromszögekben a szögek

45^{\circ}

-osak (tehát

B_{1} D_{1} = B_{1} D_{2} = C_{2} D_{2} = C_{2} D_{3} = ...

s. í. t) Minthogy

C_{2} A_{1} D_{2} ∢ = 45^{\circ}

és

A_{1} D_{2} C_{2} ∢ = 67, 5^{\circ}

, kell, hogy

A_{1} D_{2} C_{2} ∢ = 67, 5^{\circ} = α_{1}

legyen, azaz

A_{1} D_{2} = A_{1} C_{2} = x

. A

B_{1} C_{1} D_{1}

egyenlőszárú háromszögben az alapon fekvő szögek mindegyike

45^{\circ}

fele, azaz

22,5

. Kössük össze már most pl. a

C_{1}

pontot az

O

ponttal, a szabályos nyolcszög és a négyzet közös középpontjával.

O C_{1}

D_{1} D_{8}

alapon álló két egyenlőszárú háromszög ‐

O D_{1} D_{8}

és

C_{1} D_{1} D_{8} Δ

‐ csúcsait köti össze, tehát felezi ezen csúcsainál fekvő szögeket. Ebből következik, hogy

\begin{matrix} A_{1} O C_{1} ∢ = 45^{\circ} + 22, 5^{\circ} = A_{1} C_{1} O ∢ \end{matrix}

és így

\begin{matrix} A_{1} O = A_{1} C_{1} \end{matrix}

azaz:

\begin{matrix} \frac{1}{2} a \sqrt[]{2} = a - x, tehát x = \frac{a}{2} (2 - \sqrt[]{2}) = A_{1} A_{2} - A_{1} O . \end{matrix}

Ezzel meg is kaptuk az

x

, ill. a szab.

D_{1} ... D_{8}

sokszög szerkesztését!

2^{0}

. Amint láttuk,

A_{1} D_{2} = x

. Így

O D_{2} = A_{1} O - x = \frac{a \sqrt[]{2}}{2} - \frac{a}{2} (2 - \sqrt[]{2})

, tehát

O D_{2} = a (\sqrt[]{2} - 1)

és

a_{8} = D_{1} D_{2} = 2 O D_{2} sin 22, 5^{\circ} = 2 a (\sqrt[]{2} - 1) sin 22, 5^{\circ}

.
A szabályos nyolcszög apothemája

h = O D_{2} cos 22, 5^{\circ} = a (\sqrt[]{2} - 1) cos 22, 5^{\circ}

.
Eszerint a

D_{1} D_{2} ... D_{8}

sokszög kerülete^{$^{*}$}, ill, területe

\begin{matrix} k_{1} = 16 a (\sqrt[]{2} - 1) sin 22, 5^{\circ} = 16 a (\sqrt[]{2} - 1) \frac{\sqrt[]{2 - \sqrt[]{2}}}{2} = 8 a \sqrt[]{10 - 7 \sqrt[]{2}} \\ t_{1} = 8 \cdot \frac{D_{1} D_{2}}{2} h = 4 \cdot 2 a (\sqrt[]{2} - 1) sin 22, 5^{\circ} \cdot a (\sqrt[]{2} - 1) cos 22, 5^{\circ} = 4 a^{2} (3 - 2 \sqrt[]{2}) sin 45^{\circ} = \\ = 2 a^{2} (3 - 2 \sqrt[]{2}) \sqrt[]{2} = a^{2} (6 \sqrt[]{2} - 8) . \end{matrix}

A nyolcszögnek az

A_{1} A_{3}

és

A_{2} A_{4}

átlókon fekvő csúcsai egy négyzetet határoznak meg,

D_{2} D_{4} D_{6} D_{8}

-at. Ezen négyzet félátlója

O D_{2} = a (\sqrt[]{2} - 1)

és így ezen négyzet oldala, pl.

\begin{matrix} D_{2} D_{4} = a' = a (\sqrt[]{2} - 1) \sqrt[]{2} = a (2 - \sqrt[]{2}) . \end{matrix}

Ebből következik, hogy ezen négyzetbe, az előbbihez hasonló módon szerkesztett szabályos nyolcszög oldala az előbbi-nyolcszög oldalának

(2 - \sqrt[]{2})

-szerese s. i. t. Azaz: a feladatban körülírt módon keletkező szabályos nyolcszögek kerületei oly mértani haladvány tagjai, melynek hányadosa

q = 2 - \sqrt[]{2}

, területei pedig oly mértani haladványt alkotnak, melynek hányadosa

q' = {(2 - \sqrt[]{2})}^{2} = 6 - 4 \sqrt[]{2}

. Látható, hogy

0 < q < 1

és

0 < q' < 1

; tehát mindakét végtelen mértani sor összetartó.
Eszerint a végtelen sok nyolcszög kerületének összege :

\begin{matrix} K = \frac{k_{1}}{1 - q} = \frac{8 a \sqrt[]{10 - 7 \sqrt[]{2}}}{1 - 2 + \sqrt[]{2}} = \frac{8 a \sqrt[]{10 - 7 \sqrt[]{2}}}{\sqrt[]{2} - 1} = \frac{8 a (\sqrt[]{2} - 1) \sqrt[]{2 - \sqrt[]{2}}}{\sqrt[]{2} - 1} = 8 a \sqrt[]{2 - \sqrt[]{2}} . \end{matrix}

A területek összege pedig

\begin{matrix} T = \frac{t_{1}}{1 - q'} = \frac{a^{2} (6 \sqrt[]{2} - 8)}{1 - 6 + 4 \sqrt[]{2}} = \frac{a^{2} (6 \sqrt[]{2} - 8)}{4 \sqrt[]{2} - 5} = \frac{a^{2} (6 \sqrt[]{2} - 8) (4 \sqrt[]{2} + 5)}{32 - 25} = \frac{a^{2} (8 - 2 \sqrt[]{2})}{7} . \end{matrix}

Nagy Elemér (Ciszterci Szent Imre g. VII., Bp. XI.)

^{$^{*}$}A szögei azonban csak váltakozva egyenlők. Két szomszédos szög összege

270^{\circ}

^{$^{*}$} $sin 22, 5^{\circ} = \sqrt[]{\frac{1 - cos 45^{\circ}}{2}} = \frac{\sqrt[]{2 - \sqrt[]{2}}}{2}$ és ${(\sqrt[]{2} - 1)}^{2} (2 - \sqrt[]{2}) = (3 - 2 \sqrt[]{2}) (2 - \sqrt[]{2}) = 10 - 7 \sqrt[]{2} .$ Tehát $(\sqrt[]{2} - 1) \sqrt[]{2 - \sqrt[]{2}} = \sqrt[]{10 - 7 \sqrt[]{2}} .$