Feladat:	1314. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bluszt Ernő ,  Fehér György ,  Halász Iván ,  Kemény Miklós ,  Kiss J. ,  Marosán Zoltán ,  Morvay Sándor ,  Nagy Elemér ,  Papp István ,  Sebestyén Gyula ,  Tóth V. ,  Vajda József ,  Weisz Alfréd
Füzet:	1937/május, 285. oldal		PDF  |  MathML
Témakör(ök):	Csillagászati, földrajzi feladatok, Gömbi geometria, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1937/március: 1314. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.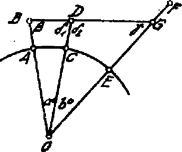     Ábránk szerint $h_1=AB$, $h_2=CD$, $h_3=EF$. Az $AB$ hegy $B$ csúcsából a $D$ csúcson átmenő sugár $EF$-t a $G$ pontban metszi: a $CD$ hegy az $EF$ hegy $EG$ részét takarja. Ezt kell kiszámítanunk. Ezen célból $OG$-t kell előbb ismernünk. $OG$ kiszámítása az $ODG$ vagy $OBG\Delta$-ből eszközölhető; előbb azonban meg kell határoznunk az $OBD\Delta$-ben a $BD$ oldalon fekvő szögeket. Ugyanis az $OBD\Delta$-ben ismeretes két oldal, $OB$ és $OD$ továbbá az általuk bezárt szög: ${\alpha }^{\circ }$. Eszerint ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(OD+OB\right):\left(OD-OB\right)=\text{tg}\frac{{180}^{\circ }-{\alpha }^{\circ }}{2}:\text{tg}\frac{\beta -{\delta }_1}{2}}\hfill \\ \hfill {\displaystyle 12737\mathrm{,}5:0\mathrm{,}5=\text{tg }{89}^{\circ }30\text{'}:\text{tg}\frac{\beta -{\delta }_1}{2}}\hfill \\ \hfill {\displaystyle \text{tg}\frac{\beta -{\delta }_1}{2}=\frac{\text{tg}{89}^{\circ }30\text{'}}{25475}\mathrm{.}}\hfill \end{array}}$ Innen $\begin{array}{c}{\displaystyle \frac{\beta -{\delta }_1}{2}=0^{\circ }15\text{'}30\text{'}\text{'}\mathrm{.}}\end{array}$ Azonban $\begin{array}{c}{\displaystyle \frac{\beta +{\delta }_1}{2}={89}^{\circ }30\text{'}}\end{array}$ és így $\beta ={89}^{\circ }45\text{'}30\text{'}\text{'}$, ${\delta }_1={89}^{\circ }14\text{'}30\text{'}\text{'}$, ${\delta }_2={90}^{\circ }45\text{'}30\text{'}\text{'}$ és $\gamma ={87}^{\circ }44\text{'}30\text{'}\text{'}$. Most már az $ODG\Delta$-ből $\begin{array}{c}{\displaystyle OG=\frac{OD\text{sin}{\delta }_2}{\text{sin}\gamma }=\frac{6369\text{sin}{90}^{\circ }45\text{'}30\text{'}\text{'}}{\text{sin}{87}^{\circ }44\text{'}30\text{'}\text{'}}=6373\mathrm{,}3\text{ km}\mathrm{.}}\end{array}$ Tehát $\begin{array}{c}{\displaystyle EG=OG-OE=6373\mathrm{,}3-6366=7\mathrm{,}3\text{ km}\mathrm{.}}\end{array}$ Eszerint az $EF$-ből még $GF=8800-7300=1500$ m látszik.    Kemény Miklós (Berzsenyi Dániel rg. VI. o. Bp. V.)   Jegyzet. A Föld görbületének figyelembe vétele nélkül természetesen jóval nagyobb rész látszana még az $EF$ hegyből $A$ csúcsról nézve (kb. 5000 m).