Kezdőlap


Feladat:	1313. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Czinczenheim József , Frankl Otto , Gálfi János , Harsányi János , Holzer Pál , Komlós János , Krisztonosich Jenő , Vajda József
Füzet:	1937/május, 283 - 284. oldal		PDF \| MathML
Témakör(ök):	Beírt háromszög, Inverzió, Mértani helyek, Kör egyenlete, Egyenes, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1937/március: 1313. matematika feladat

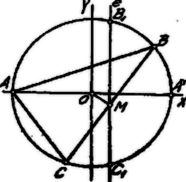
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Koordinátarendszerünk kezdőpontja a kör középpontja legyen és az $X$ -tengely az $A$ ponton menjen keresztül; az $A$ koordinátái; ( $- r$ , $0$ ) és a kör egyenlete $x^{2} + y^{2} = r^{2}$ .

B

pont koordinátái legyenek (

x_{1}

y_{1}

), a

C

ponté (

x_{2}

y_{2}

). Ekkor

\begin{matrix} {\bar{A B}}^{2} + {\bar{A C}}^{2} = {(x_{1} + r)}^{2} + y_{1}^{2} + {(x_{2} + r)}^{2} + y_{2}^{2} = k^{2} \\ (x_{1}^{2} + y_{1}^{2}) + (x_{2}^{2} + y_{2}^{2}) + 2 r (x_{1} + x_{2}) + 2 r^{2} = k^{2} \end{matrix}

Minthogy a

B

C

pontok a körön vannak,

\begin{matrix} x_{1}^{2} + y_{1}^{2} = r^{2}, x_{2}^{2} + y_{2}^{2} = r^{2} \end{matrix}

és így

\begin{matrix} x_{1} + x_{2} = \frac{k^{2} - 4 r^{2}}{2 r} . \end{matrix}

B C

távolság

M

felezőpontjának abscissája

\begin{matrix} x = \frac{x_{1} + x_{2}}{2} = \frac{k^{2} - 4 r^{2}}{4 r}, \end{matrix}

azaz állandó: az

M

pont az

X

-tengelyre merőleges

e

egyenes pontja. Azonban az

M

pont ezen egyenesnek csak a körön belül eső részét, a

B_{1} C_{1}

húrt írja le: az

M

pont mértani helye a

B_{1} C_{1}

húr.^{$^{*}$}

2^{\circ}

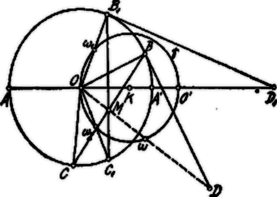
. Ismeretes, hogy a parabola gyújtópontjából a parabola valamely érintőjére bocsátott merőleges talppontja a csúcsérintőn fekszik. Eszerint a

B C

egyenesek oly parabola érintői, amelynek gyújtópontja a kör

O

pontja és csúcsérintője az

e

egyenes, tehát ezen parabola, ill. ennek egy íve a

B C

egyenesek burkolója. A szóbanforgó ív végpontjai a

B_{1}

, ill.

C_{1}

pontokból húzott érintők érintéspontjai.

3^{\circ}

. Az

O B C Δ

köré írt kör középpontja legyen

ω

és ezen körben az

O

-val diametrálisan szembenfekvő pont

D

. Ekkor az

O C D Δ

C

-nél derékszögű és ezért

\bar{O D} \cdot \bar{O M} = {\bar{O C}}^{2} = r^{2}

. Azonban

O D = 2 O ω

, tehát

O ω \cdot O M = \frac{r^{2}}{2}

. Ezen kapcsolat azt fejezi ki, hogy

ω

M

inverz pontja az

O

pólusra nézve; az inverzió hatványa

\frac{r^{2}}{2}

. Eszerint az

ω

e

egyenes inverz alakzatjának, tehát oly

γ

körnek a pontja, mely

O

-n megy keresztül és középpontja az

e

-re merőleges

O X

egyenesen fekszik. Mivel azonban az

M

pont mértani helye az

e

egyenes

B_{1} C_{1}

darabja, az inverz körnek is csak azon íve lesz az

ω

mértani helye, melyet az

O B_{1}

és

O C_{1}

egyenesek metszenek ki belőle (a

γ

körnek

ω_{1} O' ω_{2}

íve).
A

γ

kör

O X

egyenesen fekvő átmérőjének egyik végpontja

O

, a másik végpontját az

O

körhöz, a

B_{1}

pontjában húzott érintő határozza meg.
Ha ezen érintő

O X

-t a

D_{1}

-ben metszi, akkor

O D_{1}

felezőpontja lesz a

γ

átmérőjének másik végpontja,

O'

Komlós János (Gr. Széchenyi I. gyakorló r. VIII. o. Pécs)

^{$^{*}$}Az

M

pont

B_{1}

-be, ill.

C_{1}

-be esik, ha

B

és

C

összeesnek a

B_{1}

, ill.

C_{1}

pontban. A

k^{2}

ugyanazon értéke mellett a

B

és

C

pontok feküdhetnek az

A A'

átmérő ugyanazon és ellenkező oldalán.
Minthogy

A B

és

A C

a kör húrjai, egyik sem lehet

2 r

-nél nagyobb, tehát

\begin{matrix} k^{2} = {\bar{A B}}^{2} + {\bar{A C}}^{2} \leq 4 r^{2} + 4 r^{2}, k^{2} \leq 8 r^{2} . \end{matrix}

k^{2} = 8 r^{2}

, akkor csak

A B = A C = 2 r

lehetséges. A

B

és

C

pontok az

A'

pontba esnek, ugyanide esik az

M

pont is. (

B_{1} C_{1} = 0

x = r

).
Ha

4 r^{2} < k^{2} < 8 r^{2}

, akkor az

e

egyenes

O

és

A'

között metszi az

A A'

átmérőt.
Ha

k^{2} = 4 r^{2}

, akkor

{\bar{A B}}^{2} + {\bar{A C}}^{2} = 4 r^{2}

, az

A B C Δ

-ek derékszögűek; a

B C

átfogó minden helyzetében az

O

ponton megy keresztül. Az

M

pont mértani helye az

O

pontba zsugorodik össze.