Kezdőlap


Feladat:	1303. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bencze József , Cseh Sándor , Gálfi János , Lóránd Endre , Mandl Béla , Nagy Elemér , Pálos Peregrin , Radovics György , Seidl Gábor , Szabó L. , Vajda József
Füzet:	1937/április, 250 - 252. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Gyökök és együtthatók közötti összefüggések, Középponti és kerületi szögek, Szögfelező egyenes, Körülírt kör, Terület, felszín, Húrnégyszögek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1937/február: 1303. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Számításunkat rendezzük be úgy, hogy ezzel egyszersmind a következő feladatban kijelölt szerkesztést is elvégezhessük.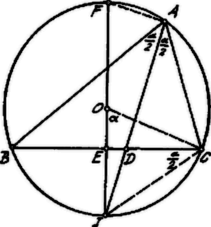
Adva lévén az $a$ oldal és az $α$ szög, megszerkesztjük a keresett háromszög köré írt kört, melynek a $B C$ húrra merőleges átmérője, ábránk szerint $I F = 2 O I = 2 O C = \frac{α}{sin α}$ .

A D = l_{α}

szögfelező keresztülmegy a

\hat{B C}

ív

I

felezőpontján. Az

A D E F

négyszögnek két szembenfekvő szöge, az

A

és

E

csúcsoknál, derékszög, tehát

A D E F

húrnégyszög. Ebből következik, hogy

\begin{matrix} \bar{I A} \cdot \bar{I D} = \bar{I E} \cdot \bar{I F} ... \end{matrix}

(1)

Adataink szerint

\begin{matrix} I A - I D = l_{α} ... \end{matrix}

(2)

I C F

derékszögű háromszögben

\begin{matrix} \bar{I E} \cdot \bar{I F} = {\bar{I C}}^{2} \end{matrix}

tehát

\begin{matrix} \bar{I A} \cdot \bar{I D} = {\bar{I C}}^{2} ... \end{matrix}

(3)

A 2) és 3) egyenletekből^{$^{*}$}

\begin{matrix} I D & = \sqrt[]{\frac{l^{2}}{4} + {\bar{I C}}^{2}} - \frac{l}{2} ... & (4) \\ I A & = \sqrt[]{\frac{l^{2}}{4} + {\bar{I C}}^{2}} + \frac{l}{2} ... & (5) \end{matrix}

ahol

\begin{matrix} I C = \frac{a}{2 cos \frac{α}{2}} . \end{matrix}

Ezek után áttérhetünk az

A B = c

és

A C = b

oldalak kiszámítására.
Minthogy
az

A B I Δ

-ből:

\begin{matrix} {\bar{A B}}^{2} + {\bar{A I}}^{2} - 2 \bar{A B} \cdot \bar{A I} cos \frac{α}{2} = {\bar{B I}}^{2} \end{matrix}

A C I Δ

-ből:

\begin{matrix} {\bar{A C}}^{2} + {\bar{A I}}^{2} - 2 \bar{A C} \cdot \bar{A I} cos \frac{α}{2} = {\bar{C I}}^{2} \end{matrix}

továbbá

B I = C I

, nyilvánvaló, hogy

A B = c

és

A C = b

\begin{matrix} x^{2} - 2 x \cdot I A \cdot cos \frac{α}{2} + {\bar{I A}}^{2} - {\bar{I C}}^{2} = 0 ... \end{matrix}

(6)

egyenlet gyökei. Minthogy 5) szerint (és a geometriai jelentést is tekintve)

I A \geq I C

, a 6) egyenlet gyökei, ha valósak, egyszersmind pozitívek, határesetben az egyik gyök zérus.
A gyökök valósak, ha

\begin{matrix} {\bar{I A}}^{2} cos^{2} \frac{α}{2} - ({\bar{I A}}^{2} - {\bar{I C}}^{2}) = {\bar{I C}}^{2} - {\bar{I A}}^{2} sin^{2} \frac{α}{2} \geq 0, ill. I C \geq I A sin \frac{α}{2} . \end{matrix}

Helyettesítve

I C

értékét:

\frac{a}{2 cos \frac{α}{2}} \geq I A sin \frac{α}{2}

, tehát

I A \geq \frac{a}{sin α}

.
Valóban az

I A

húr kisebb tartozik lenni a kör átmérőjénél.

Már most:

\begin{matrix} \sqrt[]{\frac{l^{2}}{4} + \frac{a^{2}}{4 cos^{2} \frac{α}{2}}} + \frac{l}{2} \leq \frac{a}{sin α}, \\ \frac{l^{2}}{4} + \frac{a^{2}}{4 cos^{2} \frac{α}{2}} \leq {(\frac{a}{sin α} - \frac{l}{2})}^{2}, \frac{a^{2}}{4 cos^{2} \frac{α}{2}} \leq \frac{a^{2}}{sin^{2} α} - \frac{a l}{sin α} . \end{matrix}

Ezen egyenlőtlenséget

l

szerint megoldva

\begin{matrix} l \leq \frac{a}{sin α} - \frac{a}{2} tg \frac{α}{2} . \end{matrix}

Azonban

\frac{a}{2} tg \frac{α}{2} = I E

, tehát

l \leq I F - I E

azaz

\begin{matrix} l_{α} \leq E F . \end{matrix}

Ez a feltétele annak, hogy feladatunknak legyen megoldása. A 6) egyenletből

\begin{matrix} x = I A cos \frac{α}{2} \pm \sqrt[]{\frac{a^{2}}{4 cos^{2} \frac{α}{2}} - {\bar{I A}}^{2}} sin^{2} \frac{α}{2} \end{matrix}

x

egyik értéke

b

, a másik értéke

c

. Az

I A

értéke 5) alatt van megadva.

II. Megoldás. A cosinus-tétellel

\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c cos α = {(b + c)}^{2} - 4 b c cos^{2} \frac{α}{2} ... \end{matrix}

(1)

l

szögfelező által alkotott két háromszög területének összege az egész háromszög területével egyenlő, azaz

\begin{matrix} \frac{b l}{2} sin \frac{α}{2} + \frac{c l}{2} sin \frac{α}{2} = \frac{b c}{2} sin α és innen b + c = \frac{2 b c}{l} cos \frac{α}{2} ... \end{matrix}

(2)

2) alapján

b + c

értékét 1)-be helyettesítve, keletkezik

\begin{matrix} 4 b^{2} c^{2} cos^{2} \frac{α}{2} - 4 b c l^{2} cos^{2} \frac{α}{2} - a^{2} l^{2} = 0 ... \end{matrix}

(3)

Ezen

(b c)

-re másodfokú egyenletnek gyökei mindig valósak és ellenkező előjelűek; közülük csak a pozitív felel meg, úgy hogy

\begin{matrix} b c = \frac{l^{2} cos \frac{α}{2} + l \sqrt[]{l^{2} cos^{2} \frac{α}{2} + a^{2}}}{2 cos \frac{α}{2}} ... \end{matrix}

(4)

és így

\begin{matrix} b + c = l cos \frac{α}{2} + \sqrt[]{l^{2} cos^{2} \frac{α}{2} + a^{2}} ... \end{matrix}

(5)

5) szerint

b + c > a

. Már most

b

és

c

egy másodfokú egyenlet gyökei. A rövidség kedvéért legyen

\begin{matrix} b + c = u és b c = v u, ahol v = \frac{l}{2 cos \frac{α}{2}} . \end{matrix}

Ekkor

\begin{matrix} b = \frac{u \pm \sqrt[]{u^{2} - 4 v u}}{2}, c = \frac{u \mp \sqrt[]{u^{2} - 4 v u}}{2} . \end{matrix}

A gyökök valósak, ha

u \geq 4 v

, azaz, ha

\begin{matrix} l cos \frac{α}{2} + \sqrt[]{l^{2} cos^{2} \frac{α}{2} + a^{2}} \geq \frac{2 l}{cos \frac{α}{2}}, ill. \sqrt[]{l^{2} cos^{2} \frac{α}{2} + a^{2}} \geq \frac{2 l}{cos \frac{α}{2}} - l cos \frac{α}{2} . \end{matrix}

Minthogy

\frac{2 l}{cos \frac{α}{2}} > l cos \frac{α}{2}

, négyzetre emelhetünk és így

\begin{matrix} l^{2} cos^{2} \frac{α}{2} + a^{2} \geq \frac{4 l^{2}}{cos^{2} \frac{α}{2}} - 4 l^{2} + l^{2} cos^{2} \frac{α}{2} vagyis 4 l^{2} {tg}^{2} \frac{α}{2} \leq a^{2}, \end{matrix}

tehát

\begin{matrix} l \leq \frac{a}{2} cotg \frac{α}{2} \end{matrix}

a feltétele annak, hogy legyen valós megoldás.

Bencze József (Bencés g. VIII. o. Kőszeg).

^{$^{*}$}A következőkben az

l

melletti

α

indexet a rövidség kedvéért elhagyjuk.

^*Ezen kifejezés l $\leq$ $\frac{a}{2}$ cotg $\frac{α}{2}$ alakra hozható.