Kezdőlap


Feladat:	1301. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gálfi János , Holzer Pál , Krisztonosich Jenő , Lóránd Endre , Nagy Elemér , Pálos Peregrin , Puky Gyula , Tésy Gabriella , Vajda József
Füzet:	1937/április, 247 - 248. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Kúpszeletek érintői, Ellipszis, mint mértani hely, Hiperbola, mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1937/február: 1301. matematika feladat

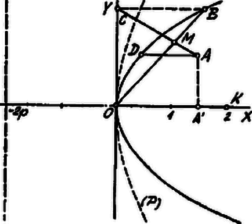
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A$ pont koordinátái legyenek $α$ , $β$ , és a változó $O B$ egyenes egyenlete

\begin{matrix} y - m x = 0 ... \end{matrix}

(1)

B

pont ordinátája^{$^{*}$} az

y^{2} = \frac{2 p y}{m}

egyenletből:

\frac{2 p}{m}

. Ugyanez a

C

pont ordinátája is. Az

A C

egyenes egyenlete:

\begin{matrix} y - β = \frac{\frac{2 p}{m} - β}{- α} (x - α) ... \end{matrix}

(2)

Az 1) és 2) egyenesek

M

metszéspontjának koordinátáit, mint

m

függvényeit számíthatjuk ki az 1) és 2) egyenletekből. Ha pedig e két egyenletből kiküszöböljük

m

-t, az

M

pont koordinátái között kapunk egy egyenletet, az

M

pont mértani helyének egyenletét. 1)-ből

m = \frac{y}{x}

; ha ezt 2)-be helyettesítjük és rendezünk, keletkezik:

\begin{matrix} a y (y - β) + (2 p x - β y) (x - α) = 0. \end{matrix}

(3)

ill.

\begin{matrix} 2 p x^{2} - β x y + α y^{2} - 2 p α x = 0 ... \end{matrix}

(3a)

Eszerint az

M

pont mértani helye kúpszelet. A 3)-ból látjuk, hogy keresztül megy az

(x = α

y = β)

, azaz az

A

ponton, az

(x = α

y = 0)

ponton ‐ ez az

A

vetülete az

X

-tengelyen, az

(y = β, x = \frac{β^{2}}{2 p})

ponton, ‐ azon a

D

ponton, amelyben az

X

-tengellyel párhuzamos

A D

metszi az adott parabolát.
A 3a)-ból pedig látjuk, hogy a kúpszelet az

Y

-tengelyt az

O

pontban érinti; ugyanis ha

x = 0

, akkor

α y^{2} = 0

, azaz

y^{2} = 0

: a kúpszelet két összeeső pontban metszi az

Y

-tengelyt.

Hogy a kúpszelet nemét megállapítsuk, vizsgáljuk elsősorban a másodfokú tagok együtthatóiból alkotott kifejezést:

\begin{matrix} δ = 2 p α - \frac{β^{2}}{4} ... \end{matrix}

(4)

I. Parabolát kapunk, ha

δ = 0

, azaz ha

β^{2} = 8 p α

. Ez annyit jelent, hogy ha az

A

pont az

y^{2} = 8 p x

parabolának pontja, az

M

pont mértani helye parabola. Ha az

A

pont

O

-ba kerül

(α = 0

β = 0)

, akkor a 3a)-ból

2 p x^{2} = 0

keletkezik, azaz

x^{2} = 0

: az

Y

-tengellyel összeeső két egyenessel van dolgunk.
Az

y^{2} = 8 p x

parabola jele legyen

(P)

. A

(P)

pontjainak ordinátái az

y^{2} = 2 p x

pontjaihoz tartozó ordináták kétszeresei.

II. Ellipszist kapunk, ha

δ > 0

, tehát ha az

A

pont a

(P)

parabolán belül fekszik.^{$^{*}$} Az ellipszisből kör lesz, ha

β = 0

és

α = 2 p

, azaz az

A

pont az

X

tengelynek

(2 p

0)

koordinátákhoz tartozó

K

pontja.

(2 p = 4 O F)

III. Hiperbolát kapunk, ha

δ > 0

, tehát ha az

A

pont a

(P)

parabolán kívül fekszik. Az

Y

-tengelyen fekvő

A

pontokra nézve

α = 0

és a hiperbola ekkor

\begin{matrix} x (2 p x - β y) = 0 \end{matrix}

egyenespárrá fajul.
Egyenlőoldalú lesz a hiperbola, ha

α = - 2 p

, ha az

A

pont az

X

-tengelyre merőleges

x = - 2 p

egyenesen fut végig.

Vajda József (Faludi Ferenc rg. VIII. o. Szombathely.)

^{$^{*}$}az

y^{2} = 2 p x

és

y - m x = 0

egyenletekből

x

kiküszöbölése után.

^{$^{*}$}Ezen ellipszis mindig valós ellipszis; ugyanis az ellipszis az $x$ minden értéke mellett az $X$ tengelyt két pontban metszi. 3)-ból, ha $y = 0$ , akkor $2 p x (x - α) = 0$ ; a két metszéspont egyike szilárd pont, t. i. $x = 0$ (az origo), a másik változó: $x = α$ abscissához tartozik; ez az $A$ pont vetülete az $X$ -tengelyen. ‐ Azt is megállapíthatjuk, hogy az origón átmenő bármely egyenes ‐ az origón kívül még egy pontban metszi az ellipszist.