Kezdőlap


Feladat:	1291. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Földesi T. , Harsányi János , Tésy Gabriella , Vajda József
Füzet:	1937/április, 254 - 256. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt háromszög, Egyenlő szárú háromszögek geometriája, Négyzetek, Feladat
Hivatkozás(ok):	Feladatok: 1937/január: 1291. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Induljunk ki az $A B C D$ négyzet valamely csúcsából, pl. az $A$ -ból. Ha $A$ a négyzetbe írt egyenlőoldalú háromszög csúcsa, a másik két csúcs az $A C$ átlóra nézve szimmetrikus helyzetű úgy, hogy az egyik csúcs $B_{1}$ a $B C$ , a másik $C_{2}$ a $C D$ oldalon fekszik és

\begin{matrix} B_{1} A B ∢ = C_{2} A D ∢ = 15^{\circ} . \end{matrix}

Ezért

A B_{1} = A C_{2}

és

B_{1} A C_{2} ∢ = 60^{\circ}

: az

A B_{1} C_{2} Δ

egyenlőoldalú.

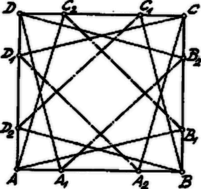
Ha már most minden csúcsból oly egyeneseket húzunk, amelyek a csúcsban találkozó oldalakkal

15^{\circ}

-ú szögeket zárnak be, az

A B

oldalon az

A_{1}

A_{2}

, a

B C

oldalon a

B_{1}

B_{2}

, a

C D

oldalon a

C_{1}

C_{2}

és a

D A

oldalon a

D_{1}

D_{2}

pontokhoz jutunk.
Már most mozogjon a

P

pont az

A B

oldalon és vizsgáljuk, hol helyezkednek a négyzetbe írt

P Q R

egyenlőoldalú háromszög

P

R

csúcsai?
Amíg

P

A A_{1}

közön fut végig, a

Q

pont a

B C

oldalon a

B_{1} B_{2}

közön, az

R

csúcs a

C D

oldalon a

C_{2} D

közön halad végig. Ha

P

A_{1} A_{2}

közön, akkor

Q

B_{2} C

R

D D_{1}

közön, ha pedig

P

A_{2} B

közön, akkor

Q

C C_{1}

és

R

D_{1} D_{2}

közön fut végig. Hasonlóan áll a dolog, ha

P

a négyzet többi oldalán fut végig. A

P Q R Δ

csúcsai közül kettő mindig a négyzet két szembefekvő oldalán helyezkedik el.

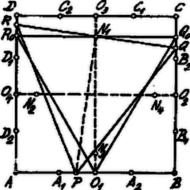
Vegyük azon esetet, amidőn

P

A_{1} A_{2}

köznek valamely pontja, még pedig legyen ez először az

O_{1}

pont, az

A B

ill.

A_{1} A_{2}

felezőpontja. A szóbanforgó egyenlőoldalú háromszög másik két csúcsának,

Q_{0}

- és

R_{0}

-nak szimmetrikusaknak kell lenniük az

A B

-t merőlegesen felező egyenesre nézve, tehát

Q_{0} R_{0} = A B

, azaz az

O_{1}

-ből kiinduló szabályos háromszög oldalának a négyzet oldalával kell egyenlőnek lennie.

Q_{0} R_{0}

felezőpontja legyen

N_{1}

. Ekkor

O_{1} N_{1}

A B = a

oldalú szabályos háromszög magassága, tehát

O_{1} N_{1} = a \frac{\sqrt[]{3}}{2}

^{$^{*}$}.
Ha most

P

A_{1} A_{2}

köz tetszőleges pontja és az onnan kiinduló szabályos háromszög másik két csúcsa

Q

és

R

, akkor

Q R

felezőpontja ugyancsak az

A B

-t merőlegesen felező egyenesen fekszik.^{$^{*}$} Legyen ez

N'

; kimutatjuk, hogy

N' \equiv N_{1}

. Húzzunk az

N'

ponton keresztül

A B

-vel párhuzamosat,

Q' R'

-t;

Q' R' = a

. Mivel

P N' ⊥ Q R

és

O' N' ⊥ Q' R'

, nyilván

P N' O_{1} Δ \sim R N' R' Δ

és így

\begin{matrix} P N' : O_{1} N' = R N' : R' N' azaz P Q \frac{\sqrt[]{3}}{2} : O_{1} N' = \frac{1}{2} P Q : \frac{1}{2} a \end{matrix}

és innen

\begin{matrix} O_{1} N' = a \frac{\sqrt[]{3}}{2}, tehát O_{1} N' = O_{1} N_{1} ill. N' \equiv N_{1} . \end{matrix}

Eszerint a változó

P Q R

szabályos háromszög

Q R

oldala, melynek

P

csúcsa az

A_{1} A_{2}

közön van, keresztülmegy a szilárd

N_{1}

ponton. Ebből tehát adódik a szerkesztés:
1) Ha

P

A_{1} A_{2}

közben van, a

P N_{1}

-re az

N_{1}

pontban merőlegest állítunk és így megkapjuk a

Q

R

csúcsokat. A négyzet mindegyik oldalának felezőpontjához tartozik egy

N

pont úgy, hogy

O_{i} N_{i} = a \frac{\sqrt[]{3}}{2}

(i = 1

2

3

4)

-es ezen

N

pont a négyzetnek

O_{i}

-n áthaladó szimmetriatengelyén fekszik.
2) Ha

P

A A_{1}

közben van, akkor

P N_{2}

meghatározza a

C_{2} D

-n az

R

pontot és ennek megfelelőleg kapjuk

Q

-t a

B_{1} B_{2}

közben.
3) Ha

P

A_{2} B

közben van, akkor

P N_{4}

határozza meg a

C C_{1}

-n a

Q

pontot és ennek megfelelőleg az

R

pontot a

D_{1} D_{2}

közben.

Harsányi János (ág. ev. g. VIII. o. Bp.)

Jegyzet. A feladat eredeti szövegében sajtóhibával ,,kerületi pont'' helyett ,,területi pont'' állott. Utóbbi szövegezés mellett a szerkesztés vizsgálata jelentékenyen terjedelmesebb; minthogy a feladat kitűzője is csak ,,kerületi'' pontokra gondolt, most az előadottakra szorítkozunk, jóllehet a közölt megoldás szerzője a sajtóhibás szövegnek is megfelelőleg dolgozott.

II. Megoldás. Az előbbi megoldás bevezetésében foglaltakat szem előtt tartva, legyen

P

A B

oldal valamely pontja az

A_{1} A_{2}

közön; ekkor a

Q

B_{2} C

, az

R

D D_{1}

köz valamely pontja lesz.
Ha a

Q

-pontot

60^{\circ}

-al elforgatjuk

P

körül ‐ a pozitív irányban ‐ akkor

Q

pont az

R

-be esik; ha a

B C

-oldalt

P

körül

60^{\circ}

-kal elforgatjuk, akkor a

B C

oldal

Q

pontjának a

D A

oldal

R

pontjába kell esnie.

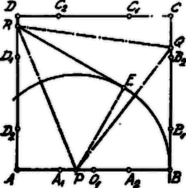
A szerkesztés ezen alapon a következő:

P B

sugárral kört szerkesztünk és ezen kijelöljük az

E

pontot úgy, hogy

B E = 60^{\circ}

legyen. Az

E

pontban a körhöz érintőt húzunk; ezen érintő helyzetét veszi fel a

B C

egyenes, ha

P

körül

60^{\circ}

-kal elforgattuk, amikor is

B

E

-be kerül. Ezen érintő a

D A

oldalt az

R

pontban metszi úgy, hogy

P R

lesz a

P

-ből kiinduló, a négyzetbe írt szab. háromszög oldala. A

P R

sugárral

P

-ből szerkesztett kör

B C

-t a

Q

pontban metszi.
Minthogy a

P B Q Δ ≅ P E R Δ

^{$^{*}$} és

P B Q Δ

60^{\circ}

-os forgatással kerül a

P E R Δ

helyzetébe, nyilván

Q P R ∢ = 60^{\circ}

és így a

P Q R Δ

egyenlőoldalú.

Tésy Gabriella (Szent Margit leányg. VIII. o. Bp. XI.)

^{$^{*}$}Az

N_{1}

pont távolsága a

C D

oldaltól

N_{1} O_{3} = Q_{0} C = \frac{B_{2} C}{2} = \frac{a tg 15^{\circ}}{2} = \frac{a (2 - \sqrt[]{3})}{2}

. Eszerint

\begin{matrix} O_{1} N_{1} + N_{1} O_{3} = \frac{a \sqrt[]{3}}{2} + \frac{a (2 - \sqrt[]{3})}{2} = a . \end{matrix}

^{$^{*}$}Vegyük $P$ -nek az $A B$ -n, $O_{1}$ -re szimmetrikus pontját. Az ehhez tartozó $P' Q' R'$ szab. háromszög a $P Q R Δ$ -gel szimmetrikus az $O_{1} O_{3}$ -ra nézve; kell tehát, hogy $Q R$ és $Q' R'$ az $O_{1} O_{3}$ ugyanazon pontján menjenek keresztül.

^{$^{*}$}Két oldal és a nagyobbikkal szemben fekvő szög $(90^{\circ})$ egyenlő