Kezdőlap


Feladat:	1287. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Gy. , Barna Tibor , Bluszt Ernő , Breuer Gy. , Czinczenheim József , Farkas Imre , Fehér György , Frankl Otto , Földesi Tamás , Gombos S. , Grosz László , Harsányi János , Herczeg Gy. , Holzer R. , Huhn Péter , Jánoshegyi F. , Kolostori J. , Komlós János , Krisztonosich Jenő , Lóránd Endre , Marosán Zoltán , Nagy Elemér , Pálos Peregrin , Papp I. , Pappert T. , Petricskó Miklós , Puky Gy. , Schwarz János , Sebestyén Gyula , Somogyi Antal , Szerényi László , Szücsi István , Taussig F. , Tésy Gabriella , Vajda József
Füzet:	1937/március, 209 - 211. oldal		PDF \| MathML
Témakör(ök):	Kör egyenlete, Harmadfokú (és arra visszavezethető) egyenletrendszerek, Egyenesek egyenlete, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1937/január: 1287. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $G_{3}$ és $G_{2}$ görbék közös pontjait az

\begin{matrix} y = 2 x^{3} - 8 x ... & (1) \\ és & y = m x^{2} - 8 x ... & (2) \end{matrix}

egyenletekből álló rendszer gyökei határozzák meg.

y

kiküszöbölésével

\begin{matrix} 2 x^{3} - 8 x = m x^{2} - 8 x ill. 2 x^{3} - m x^{2} \equiv x^{2} (2 x - m) = 0 ... \end{matrix}

(3)

Ezen egyenletnek

x = 0

kétszeres gyöke. Az

(x = 0, y = 0)

pont, azaz az origo a két görbének érintkezési pontja. Ezen kívül még

\begin{matrix} 2 x - m = 0, ill. x = \frac{m}{2}, y = \frac{m^{3}}{4} - 4 m \end{matrix}

értékpár határoz meg egy közös pontot, t. i.

A

-t. Az

O A \equiv e

egyenes egyenlete

\begin{matrix} y = \frac{m^{2} - 16}{2} x ... \end{matrix}

(4)

G_{3}

görbe zérus helyeit a

2 x^{3} - 8 x \equiv 2 x (x^{2} - 4) = 0

egyenlet gyökei szolgáltatják; ezek

x_{1} = 0

x_{2} = + 2

x_{3} = - 2

.
A zérus helyek koordinátái:

(0,0)

(+ 2, 0)

(- 2, 0)

.
A

(+ 2, 0)

pontból az

e

-re bocsátott merőleges egyenes egyenlete

\begin{matrix} y = \frac{2}{16 - m^{2}} (x - 2) ... \end{matrix}

(5)

A 4) és 5) egyenes metszéspontjának

M_{1}

-nek koordinátáit, mint

m^{2}

függvényeit kapjuk meg a 4) és 5) egyenletekből. Ha tehát e két egyenletből

m^{2}

-et kiküszöböljük,

x

és

y

, azaz az

M_{1}

koordinátái között kapunk egy egyenletet, azon görbéét, amelynek pontja

M_{1}

.
4)-ből

\begin{matrix} m^{2} = \frac{2 y + 16 x}{x}, \end{matrix}

5)-ből

\begin{matrix} m^{2} = \frac{16 y - 2 x + 4}{y} . \end{matrix}

Eszerint

\begin{matrix} \frac{2 y + 16 x}{x} = \frac{16 y - 2 x + 4}{y} ... \end{matrix}

(6)

Rendezés után

\begin{matrix} x^{2} + y^{2} - 2 x = 0, ill. {(x - 1)}^{2} + y^{2} = 1 ... \end{matrix}

(7)

azon kör egyenlete, amelynek pontja

M_{1}

. Ezen kör középpontja az

X

-tengelyen van, keresztülmegy az origon, sugara 1.
Az

M_{2}

pontra nézve pedig

\begin{matrix} {(x + 1)}^{2} + y^{2} = 1 ... \end{matrix}

(8)

oly kör egyenlete, mely az előbbivel szimmetrikus az

Y

-tengelyre nézve.
Ha t. i. a

(- 2, 0)

pontból

e

-re merőlegest bocsátunk, ennek egyenlete

\begin{matrix} y = \frac{2}{16 - m^{2}} (x - 2) . \end{matrix}

Ennek megfelelőleg 6) jobboldalán

+ 4

helyett

- 4

és így

x^{2} + y^{2} + 2 x = 0

keletkezik.
Kérdés már most: leírja-e

M_{1}

az egész körvonalat, amelynek egyenlete a 7), ill.

M_{2}

azon körvonalat, amelynek egyenlete 8)? Hogy ezen kérdésre felelhessünk, szükséges és elegendő, hogy a 4) alatti

O A \equiv e

egyenes helyzetét vizsgálhassuk, azaz ennek irányhatározója felvesz-e minden értéket

- \infty

-től

+ \infty

-ig?
Az

e

egyenes irányhatározója:

\frac{m^{2} - 16}{2}

. Ennek értéke, ha

m

változik

- \infty

-től

+ \infty

-ig,

+ \infty

-től csökken

- 8

-ig, azután növekszik

- 8

-tól

+ \infty

-ig; tehát nem veszi fel azon értékeket, melyek

- 8

és

- \infty

között vannak. Ebből következik, hogy az

e

egyenes, mely

O

körül forog, nem vesz fel minden helyzetet. Az

O

ponthoz tartozó sugársor sugarai közül kimaradnak azok, melyeknek irányhatározói

- 8

és

- \infty

között vannak. Ezen kimaradó egyeneseken fekvő

M_{1}

, ill.

M_{2}

pontok nem tartoznak a mértani helyhez. Más szóval, az

M_{1}

mértani helye a 7) alatti kör egy része; a 7) alatti körből azon ívet kell elvennünk, melyet az

y = - 8 x

egyenes vág le róla. Ezen íven fekvő pontokra nézve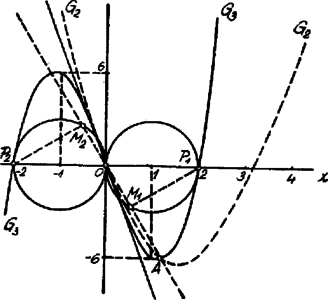

\begin{matrix} 0 < x < \frac{2}{65} és y < 0.^{1} \end{matrix}

Hasonlóan az

M_{2}

pontok mértani helye a 8) kör egy része. Ezen körből azon ívet kell elvennünk, melynek pontjaira nézve

\begin{matrix} - \frac{2}{65} < x < 0 és y > 0. \end{matrix}

(A két körből kieső ívrész szimmetrikus helyzetű az

O

pontra nézve).
Vizsgáljuk már most közelebbről a geometriai viszonyokat. A

G_{3}

oly szilárd harmadrendű parabola, mely az

X

-tengelyt a

- 2

0

+ 2

helyeken metszi; a

(0, 0)

pont a görbe inflexiós pontja és itt az érintő irányhatározója

- 8

. (Egyenlete

y = - 8 x

). A görbének

x = - 2

és

x = 0

között felső,

x = 0

és

x + 2

között alsó tetőpontja van: az előbbi koordinátái

x_{1} =_{}^{\infty} - 1, 15

y_{1} =_{}^{\infty} 6, 1

, az utóbbié

x_{2} =_{}^{\infty} + 1, 15

y_{2} =_{}^{\infty} - 6, 1

²
A

G_{2}

m

értéke szerint változó másodrendű parabola, de mindegyik keresztülmegy az origon és ezen pontban mindegyiknek érintője az

y = - 8 x

egyenes, azaz

G_{2}

és

G_{3}

(0, 0)

pontban érintkeznek.
Ha

m = 0

, akkor a

G_{2}

parabolából az

y = - 8 x

egyenes lesz.
Ha

m > 0

, akkor

G_{2}

-nek alsó tetőpontja van az

x = \frac{4}{m}

helyen.

G_{2}

G_{3}

-t az

X

-tengely pozitív oldalán metszi az

A (\frac{m}{2}, \frac{m^{3}}{4} - 4 m)

pontban. Ezen metszéspont végig fut a

G_{3}

-nak azon részén, mely az

X

-tengely pozitív oldalán fekszik. Az

O A

egyenes határhelyzete azonban az

y = - 8 x

egyenes.³
Az

y = a x

egyenesek közül azoknak, amelyekre nézve

a < - 8

, nincs a

G_{3}

görbével (az origon kivül) közös pontjuk.
Ha

m < 0

, akkor

G_{2}

-nek felső tetőpontja van az

x = \frac{4}{m}

helyen.

G_{2}

G_{3}

-t az

X

-tengely negatív oldalán metszi az

A

pontban. Ezen metszéspont végig fut a

G_{3}

-nak azon részén, mely az

X

-tengely negatív oldalán fekszik. Az

O A

egyenes határhelyzete ugyanaz, mint előbb.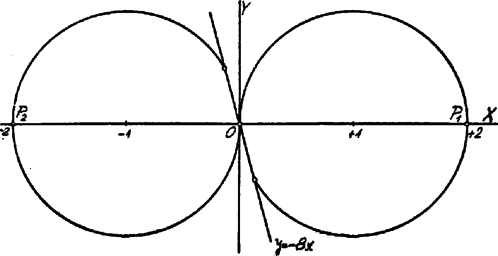

Ha az

y = a x

egyenesre⁴ a

P_{1} (2, 0)

pontból merőlegest állítunk, akkor ennek talppontja

M_{1}

, Thales tétele szerint oly körön fekszik, melynek átmérője az

O P_{1}

távolság. Az

M_{1}

azonban nem írja le ezen kört egészen: kimaradnak azon pontjai, amelyek az

y = a x

sugársor azon egyenesein feküsznek, amelyekre nézve

a < - 8

.
Ha pedig az

y = a x

egyenesre a

P_{2} (- 2, 0)

pontból állítunk merőlegest, ennek

M_{2}

talppontja oly körön fekszik, amelynek átmérője

O P_{2}

. Az

M_{2}

azonban nem írja le egészen ezen kört: kimaradnak e kör azon pontjai, amelyek az

y = a x

a < - 8

egyeneseken feküsznek.
Forgassuk az

O

ponton átmenő egyenest az

Y

-tengelynek megfelelő kezdőhelyzetből a pozitív forgási irányban, míg az

y = - 8 x

egyenes helyzetébe jut; ezen forgás közben leírt síkrészen fekvő pontjai a két körnek nem tartoznak az

M

pont mértani helyéhez.

¹Az

x^{2} + y^{2} - 2 x = 0

és az

y = - 8 x

egyenes közös pontjai az

x = 0

és

x = \frac{2}{65}

abszcisszákhoz tartoznak.

² $y = 2 x^{3} - 8 x$ esetében $y' = 6 x^{2} - 8 = 0$ , ha $x^{2} = \frac{4}{3}$ , $x =_{}^{\infty} \pm 1, 15$ .

³Ha $m = 0$ , akkor az $A$ pont $O$ -ba esik. Ekkor $O A$ a $G_{3}$ inflexiós érintője lesz.

⁴Ahol $a \geq - 8$ .