Kezdőlap


Feladat:	1276. matematika feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Barna Tibor , Bölcskei János , Czinczenheim József , Frankl Otto , Fűzy O. , Harsányi I. , Holzer Pál , Kolostori J. , Komlós János , Kondor István , Lóránd Endre , Nagy Elemér , Németh K. , Pálos Peregrin , Papp István , Schwarz János , Sebestyén Gyula , Somogyi Antal , Vajda József
Füzet:	1937/február, 179 - 180. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Vetítések, Síkgeometriai szerkesztések, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1936/december: 1276. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $O$ a parabola csúcsa, $O X$ a parabola főtengelye és ezen $F$ a gyújtópontja, $O Y \equiv c$ a csúcsérintője és a $d$ egyenes $(d ∥ c)$ a vezérvonala. A parabola tetszőleges $P$ pontjában húzott $t$ érintő a $d$ -t az $M$ , a $c$ -t az $N$ pontban metszi. A $P$ pont vetülete 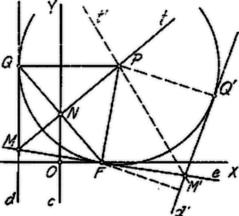$d$ -n legyen $Q$ . Nyilván $P F = P Q$ .

Ismeretes továbbá, hogy

t

felezi az

F P Q ∢

-et és

t

F Q

-t az

N

pontban felezi¹ Ebből következik, hogy

M F P Δ =_{}^{\infty} M Q P Δ

,

tehát²

M F P ∢ = M Q P ∢ = 90^{\circ}

.

Eszerint az

M F P

derékszögű háromszögben ismeretes az egyik befogó

(F P)

és a másik befogónak az átfogón való vetülete

(M N)

. Ezért

\begin{matrix} {\bar{F P}}^{2} = \bar{P N} (\bar{P N} + \bar{N M}) . \end{matrix}

Szerkesszünk tehát egy kört, melynek átmérője

N M

; a kör valamely pontjában húzzunk érintőt és az érintési pontból kiindulva mérjük rá az

F P

távolságot. Ezen távolság másik végpontjából húzzunk szelőt a kör középpontján keresztül; a szelőnek a körön kívül fekvő szelete lesz

P N

.³
Eszerint az

F P

-re az

F

pontban merőleges

e

egyenest állítunk; a

P

pontból

(P N + N M)

sugárral kört szerkesztünk, mely

e

-t az

M

(ill.

M'

pontban) metszi. Ezután a

P

pontból

P F

sugárral szerkesztünk

k

kört. Az

M

pontból a

k

körhöz húzott egyik érintő

e

, a másik a keresett

d

vezérvonal. Ugyanúgy járhatunk el az

M'

pontból kiindulva is.
A feladatnak eszerint két, az

F P

-re nézve szimmetrikus helyzetű megoldása van.

Somogyi Antal (Gyakorló g. VII. o. Bp.)

¹A

t

egyenes sz tengelye; a

P Q M F

idomnak.

²Azaz: a parabola bármely érintőjének azon darabja, mely az érintési pont és a vezérvonal között fekszik, a parabola gyújtópontjából derékszög alatt látható.

³a L. II. évf. 279. oldalán a 147. Feladat II. megoldását. (1926/5. ‐ a szerk.)