Kezdőlap


Feladat:	1267. matematika feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Barna Tibor , Czinczenheim József , Farkas Imre , Frankl Otto , Komlós János , Schwarz János , Somogyi Antal , Vajda József
Füzet:	1937/január, 151 - 152. oldal		PDF \| MathML
Témakör(ök):	Elemi függvények differenciálhányadosai, Ellipszis egyenlete, Kúpszeletek érintői, Ellipszis, mint mértani hely, Ellipszis, mint kúpszelet, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1936/november: 1267. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Jelentse $A$ a vonaldarabnak az $Y$ tengelyen, $B$ az $X$ -tengelyen mozgó végpontját. Az $A$ ill. $B$ pont által leírt ellipszis egy vonaldarabbá zsugorodik össze, az előbbi az $Y$ -, utóbbi az $X$ -tengelyen fekszik. Az $A$ ponthoz tartozó normális merőleges az $Y$ -, a $B$ ponthoz tartozó merőleges az $X$ tengelyre; ezen két merőleges metszőpontja legyen $I$ . Ki fogjuk mutatni, hogy az $A B$ tetszőleges $M$ pontjához tartozó normális az $I$ ponton megy keresztül.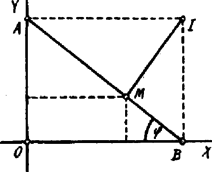

Legyen

A M = a

M B = b

A B = a + b

. A vonaldarab helyzetét az

O B A ∢ = φ

határozza meg. Ezen helyzetben az

M

pont koordinátái

(x, y)

, az

I

ponté

(x_{1}, y_{1})

, úgy hogy

\begin{matrix} x = a cos φ, y = b sin φ;^{1} \\ x_{1} = O B = (a + b) cos φ, y_{1} = O A = (a + b) sin φ . \end{matrix}

¹
Az

M I

egyenes irányhatározója:

\begin{matrix} \frac{y_{1} - y}{x_{1} - x} = \frac{(a + b) sin φ - b sin φ}{(a + b) cos φ - a cos φ} = \frac{a sin φ}{b cos φ} . \end{matrix}

M

pont által leírt ellipszis

M

pontjához tartozó normális irányhatározója

- \frac{x'}{y'}

,² ahol

y'

és

x'

jelentik

y

-nak és

x

-nek

φ

szerint képezett differenciálhányadosait és így

\begin{matrix} - \frac{x'}{y'} = \frac{a sin φ}{b cos φ} - \frac{y_{1} - y}{x_{1} - x} . \end{matrix}

Tehát az

M

ponthoz tartozó normális iránya összeesik

M I

irányával, a szóbanforgó normális az

I

ponton megy keresztül.

Frankl Ottó (izr. rg. VIII. o. Bp.)

II. Megoldás. Az előbbi megoldás bevezetésében jellemeztük az

A B

vonaldarab és az

M

pont helyzetét. Feltehetjük, hogy

A M > M B

. Legyen

C

A B

felezőpontja. Az

M

pontból

O A

-val párhuzamosan vont egyenes

O C

-t az

N

pontban metszi; ekkor

C M = C N

és így

O N = A M

, az ellipszis félnagytengelye ill. a főkör sugara. Eszerint az

N

pont a főkör azon pontja, melynek affin pontja az ellipszisen az

M

. A főkörnek

N

pontjában húzott érintője

O B

-t a

P

pontban metszi; ezért az ellipszisnek

M

pontjához tartozó érintője

M P

. Az ellipszisnek

M

pontjához tartozó normálisa

M P

-re merőleges és

O C

-t az

I

pontban metszi.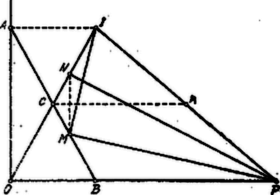

I M P

és

I N P

derékszögű háromszögek

I P

átfogójának

K

felezőpontja az

I

N

M

P

pontokon átmenő kör középpontja. Ezért az

M N

távolságot merőlegesen felező egyenes ‐ az

O B

-vel párhuzamos ‐ keresztülmegy a

K

ponton, továbbá ‐ mivel

C M = C N

‐ a

C

ponton is. Minthogy

K

felezi

I P

-t és

C K ∥ O B

, következik:

O I = 2 O C

, azaz az

M

ponthoz tartozó normális

O C

-t mindig azon szilárd

I

pontban metszi, amelyre nézve

O I = 2 O C

. (

O A I B

téglalap csúcsa

I

Komlós János (Gr. Széchenyi István gyakorló r. VII. o. Pécs).

¹Az ellipszis egyenlete

\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = cos^{2} φ + sin^{2} φ = 1

²Az érintő irányhatározója: $\frac{d y}{d x} = \frac{d y}{d φ} : \frac{d x}{d φ} = \frac{y'}{x'}$ ; a normálisé $- 1 : \frac{y'}{x'} = - \frac{x'}{y'}$ .