Kezdőlap


Feladat:	1262. matematika feladat	Korcsoport: 14-15	Nehézségi fok: -
Megoldó(k):	Barna Tibor , Czinczenheim József , Fehér György , Földesi Tamás , Harsányi János , Holzer Pál , ifj. Seidl Gábor , Jakab Károly , Kemény György , Komlós János , Miklós F. , Pálos Peregrin , Papp I. , Rusznák I. , Sebestyén Gyula , Tarnóczy Loránt , Vajda József , Weisz Alfréd , Zádor Gy. , Zöldhegyi Gy.
Füzet:	1937/január, 133 - 135. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 1936/november: 1262. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen

\begin{matrix} x + y - 1 = k, tehát x + y - 2 = k - 1 ... \end{matrix}

(1)

és vizsgáljuk az adott

a

számnak a

\begin{matrix} \frac{k (k - 1)}{2} ... \end{matrix}

(2)

alakú egész számok sorához viszonyított helyzetét.¹
Két eset lehetséges:

a

vagy előfordul ezen számok sorában, vagy a számsor két tagja között van.
Az első esetben a

k

poz. egész szám megállapítható úgy, hogy

\begin{matrix} a = \frac{(k + 1) k}{2}, azaz x = \frac{(k + 1) k}{2} - \frac{k (k - 1)}{2} = k \end{matrix}

és ekkor, mivel

x + y - 1 = k

x = k

mellett

y = 1

, tehát egyenletünket a

(k, 1)

számpár kielégíti.
A második esetben

k

meghatározható úgy, hogy

\begin{matrix} \frac{k (k - 1)}{2} < a < \frac{(k + 1) k}{2}, ... \end{matrix}

(3)

és ekkor

\begin{matrix} 0 < x < k, t.i. x = a - \frac{k (k - 1)}{2} = α, \end{matrix}

azaz létezik egy

x = α

poz. egész szám úgy, hogy

1 \leq α < k

,

és így

\begin{matrix} y = k + 1 - α > 0, \end{matrix}

egyenletünket tehát az

(a, \bar{k + 1 - α})

számpár elégíti ki.
A két eset egybefoglalásával mondhatjuk:

1 \leq α \leq k

.
Már most azt kell kimutatnunk, hogy egyenletünket több pozitív egész számokból álló számpár nem elégítheti ki. Nézzük tehát az

a

számnak a 2) sorozat azon tagjaihoz való helyzetét, melyek

\frac{k (k - 1)}{2}

-t megelőzik!¹ Így

\begin{matrix} a = \frac{k (k - 1)}{2} + α = \frac{(k - 1) (k - 2)}{2} + k - 1 + α, \end{matrix}

azaz most

\begin{matrix} x = k - 1 + α > 0; \end{matrix}

azonban, mivel

\begin{matrix} x + y - 1 = k - 1, \\ y = k - x = k - (k - 1 + α) = 1 - α \leq 0, \end{matrix}

tehát már nem kapunk pozitív

y

-t.
Általában, mivel

\begin{matrix} a = \frac{k (k - 1)}{2} + α = \frac{(k - i) (k - i - 1)}{2} + α + (k - 1) + (k - 2) + ... + (k - i) \\ és i < k, \end{matrix}

azért

\begin{matrix} x = α + i k - \frac{i (i + 1)}{2} > 0. \end{matrix}

Azonban most

\begin{matrix} x + y - 1 = k - i, \end{matrix}

tehát

\begin{matrix} y = 1 + (k - i) - x = 1 + (k - i) - α - i k + \frac{i (i + 1)}{2}, \\ y = 1 - α - (i - 1) (k - \frac{i}{2}) < 0. \end{matrix}

II. Megoldás. Ha be tudjuk bizonyítani, hogy a pozitív egész

x

y

számokból

(x, y)

számpár összes lehető változatainak megfelelő rendezésével

\begin{matrix} f (x, y) \equiv x + \frac{(x + y - 1) (x + y - 2)}{2} \end{matrix}

kifejezés a pozitív számsor összes egész számait adja,

1

-től kezdődőleg, egyszer és csak egyszer, akkor bebizonyítottuk, hogy mindig van egy és csakis egy pozitív egész

(x, y)

számokból álló

(x, y,)

számpár, amely a követelménynek megfelel. Legyen ugyanis

x + y = c

, állandó, akkor

f (x, y) = a

csak az

x

-től függ úgy, hogy amint

x

növekedik egy-egy egységgel, úgy növekedik

a

is egy-egy egységgel. Tehát az

(x, y)

számpár ama változataihoz, melyek az

x + y = c

feltételnek megfelelnek, a pozitív egész számsor egymásután következő tagjainak egy bizonyos része felel meg egyszer és csak egyszer.¹
Ha bebizonyítjuk, hogy az

(x, y)

számpár változatainak következő csoportjához, amelyre nézve

x + y = c + 1

, a pozitív egész számsornak az előbbieket közvetlenül követő csoportja felel meg, akkor beláthatjuk, hogy ha az

(x, y)

számpár változatait így rendszerezve helyettesítjük

f (x, y)

kifejezésbe, akkor valóban a pozitív egész számok teljes sorát kapjuk, egymásután, egyszer és csak egyszer,

1

-től kezdődőleg. Ugyanis, ha

x = 1

y = 1

, akkor

a = 1

.
Az

x + y = c

csoport utolsó számpárja az

x = 1

2

...

c - 1

sorrendben haladva

(\bar{c - 1}, 1)

x > c

nem lehet, mert akkor

y \leq 0

. A következő

x + y = c + 1

csoport első számpárja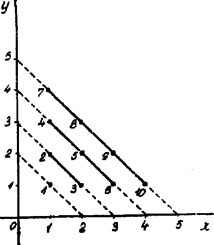

(1, c)

\begin{matrix} A (\bar{c - 1,} 1) számpárral \end{matrix}

\begin{matrix} f (x, y) = c - 1 + \frac{(c - 1) (c - 2)}{2}, azaz a_{1} = \frac{c^{2} - c}{2} . \end{matrix}

(1, c)

számpárral

\begin{matrix} f (x, y) = 1 + \frac{c (c - 1)}{2} azaz a_{2} = 1 + \frac{c^{2} - c}{2} \end{matrix}

tehát

\begin{matrix} a_{2} = a_{1} + 1. \end{matrix}

Látjuk ebből, hogy az

x + y = c

csoport utolsó számpárjának megfelelő egész szám

a_{1}

és az utána következő egész szám,

a_{2}

, tényleg a következő csoport első

(x, y)

számpárjához tartozó szám.
Ezzel tehát állításunkat bebizonyítottuk. Minthogy

x + y = c

oly egyenesnek egyenlete, mely a tengelyekről

c

darabot vág le, ezen egyenesek mentén feküsznek az

(x, y)

számpárokhoz tartozó

a

egész számok. A kezdő szám

a = 1

x + y = 2

egyenesen fekszik. Az

x + y = c

egyenesnek a tengelyeken fekvő pontjai már nem határoznak meg

a

számot.

Weisz Alfréd (Bolyai r. VII. o. Bp. V.)

¹E sorozat tagjai: 0, 1,1 3, 6, 10, 15, 21, 28

...

másodrendű számtani haladványt alkotnak, az egymásután következő tagok különbségei 1, 2, 3, 4, 5,

...

elsőrendű számtani haladványt.

¹Ha azokat tekintjük, amelyek $\frac{k (k - 1)}{2}$ után következnek, akkor már $x < 0$ .

¹Ezen tagok száma: $c - 1$ , mert, ha $x + y = c$ , akkor $x = 1$ , $2$ , $...$ $c - 1$