Feladat: 1258. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Barna T. ,  Czinczenheim J. ,  Holzer P. ,  Lóránd E. ,  Schwarz J. 
Füzet: 1936/december, 100 - 102. oldal  PDF  |  MathML 
Témakör(ök): Kör (és részhalmaza), mint mértani hely, Háromszögek szerkesztése, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1936/október: 1258. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintettel azon érdeklődésre, melyet a f. é. tanulmányi verseny II. feladata keltett, a többitől elkülönítve tárgyaljuk a feladattal kapcsolatban felmerülő kérdéseket.

 

Szerkesszünk adott háromszög köré adott oldallal bíró szabályos háromszöget! Mi a szerkesztés lehetőségének feltétele?
 

Megoldás. Legyen az adott háromszög a KLM▵; ezen háromszög köré szerkesztettük az ABC egyenlőoldalú háromszöget, adott oldallal.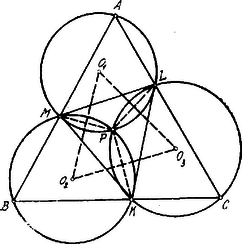
 
 

Az A, B, C csúcsoknál 60∘-ú szögek vannak: az A csúcs mértani helye oly kör íve, amelyben az LM húrhoz 60∘-ú kerületi szög tartozik, és ezen ív a háromszögön kívül fekszik. Hasonlót mondhatunk a B, ill. C csúcs mértani helyéről az MK, ill. KL oldallal kapcsolatban. Ezen mértani helyeket megszerkesztjük. A három kör egy olyan P ponton megy keresztül, amelyből a háromszög mindegyik oldala 120∘-120∘-ú szög alatt látható.
Ezen körök középpontjai O1, O2, O3. Az O1 és O2 körök közös húrja PM: erre a centrális, O1O2, merőleges. Hasonlóan O2O3⊥PK és O3O1⊥PL. Minthogy
MPK∢=KPL∢=LPM∢=120∘,
az O1O2O3▵ mindegyik szöge 60∘ és ezért
O1O2=O2O3=O3O1.

Megszerkesztve már most e három kört, azon feladat előtt állunk, hogy két‐két kör metszéspontján (K, L, M) keresztül szelőt fektessünk úgy, hogy a szelőnek a két körben fekvő darabjainak (húrok) összege adott hosszúság legyen (AB=BC=CA). Ezen összegnek azaz az egyenlő oldalú háromszög adott oldalának nagyobbnak kell lennie a KLM▵ legnagyobb oldalánál.1
Tegyük fel, hogy az O1 és O2 körök M metszéspontján keresztül az adott AB hosszúságú szelőt fektettük. Bocsássunk 01-ből és O2-ből merőlegest AB-re, P1 ill. P2 talpponttal. Ekkor 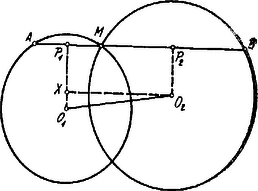P1P2=AB2.
 
 

Húzzunk O2-ből AB-vel párhuzamost, mely OP1-t az X pontban metszi; ekkor O2X=P1P2. Eszerint az O1O2X derékszögű háromszög meg van határozva. Ezt megszerkesztjük:
az O1O2 távolság, mint átmérő felett félkört szerkesztünk; ebben felmérjük az O2X=P1P2=AB2 hosszúságú húrt, majd ezen húrral az M ponton keresztül párhuzamost húzunk. Ezáltal megkapjuk az adott AB hosszúságú szelőt. Ugyanúgy felmérhetjük a szóban forgó félkörben az O1Y=O2X húrt, miáltal egy másik megoldást kapunk, amely az előbbivel szimmetrikus helyzetű az M ponton át O1O2-vel párhuzamosan vont egyenesre nézve.
 

Ha már most AB-t elhelyeztük, az A-t összekötjük az L, B-t a K ponttal. Minthogy BAL∢=ABK∢=60∘, kell, hogy ACB∢=60∘ legyen, azaz a C pont az O3 középpontú körön fekszik és az ABC▵ egyenlőoldalú, melynek oldala a megadott hosszúság.2
 

Ezen szerkesztés megköveteli azonban, hogy P1P2=AB2≤O1O2 azaz AB≤O1O2 legyen. Ha AB=2O1O2, akkor AB∥O1O2, BC∥O1O2 és CA∥O3O1.
 

A háromszög köré írható legnagyobb egyenlő oldalú háromszög oldalai párhuzamosak az O1O2O3▵ oldalaival és ezeknek kétszeresük. Eszerint a KLM▵ köré írható egyenlő oldalú háromszög oldala nem lehet nagyobb, mint 2O1O2.
 

I. Jegyzet. Ha a KLM háromszög oldalai fölé, a háromszögön kívül egyenlő oldalú háromszögeket szerkesztünk és ezeknek K', L', M' csúcsait összekötjük a KLM▵ szembenfekvő K, L, M csúcsaival, akkor a K'K, L'L, M'M egyenesek az előbb definiált P ponton mennek keresztül. Ebből következik, hogy a KLM▵ köré írt legnagyobb egyenlőoldalú háromszög oldalai a K'K, L'L, M'M egyenesekre rendre merőlegesek.
 

II. Jegyzet. Ha feladatunkat úgy értelmezzük, hogy a K, L, M pontokon keresztül oly egyeneseket húzzunk, amelyek egyenlőoldalú ABC háromszöget határoznak meg1, akkor az A, B, C pontok a KLM▵-ön belül is feküdhetnek úgy, hogy az A, B, C pontokból a KLM háromszög oldalai 120∘-120∘-ú szögek alatt láthatók. Ebben az esetben az A, B, C pontok a megoldásban definiált O1, O2, O3 köröknek, a KLM▵-ön belül levő ívein fekvő pontjai. (Az ilyen ABC▵ bármely oldala kisebb tartozik lenni a KLM▵ legkisebb oldalánál.)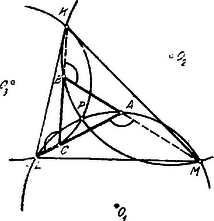
 
 

Ha pedig a KLM▵ oldalai, mint húrok fölé a megoldásban szereplő O1, O2, O3 körökkel, az illetőoldalra nézve szimmetrikus helyzetű köröket vesszük, akkor ezek oly P' pontban metszik egymást, amelyből a KLM▵ egyik oldala 120∘-ú, a másik két oldal 60∘-60∘-ú szög alatt látható.

Ha a K-ból kiinduló egyenes a KL-hez tartozó (ω3) kört γ, a KM-hez tartozó (ω2) kört a β pontban metszi, akkor
KγL∢=60∘,KβM∢=60∘.

Mβ és γL meghatározzák az α pontot úgy, hogy α=60∘ és MαL∢=120∘; tehát kell, hogy α az LM-hez tartozó ω1 körön feküdjék.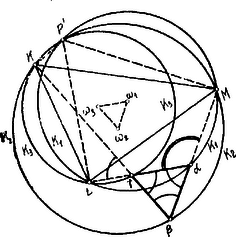
 
 

Az ABC▵ egy‐egy oldala úgy az előbbi, mint az utóbbi esetben két húr különbsége, pl.
BC=KC-KB,ill.βγ=Kβ-Kγ.

A K(L,M) ponton keresztül szelőt kell húznunk úgy, hogy a K(L,M) ponton keresztülmenő két körben fekvő darabjainak (húroknak) különbsége az egyenlőoldalú háromszög adott oldalával egyezzék meg. A szerkesztés analóg a megoldásban tárgyalt esettel.
Az ω1ω2ω3▵ egyenlőoldalú. (Ugyanis ω3ω1⊥LP', ω1ω2⊥MP', ω2ω3⊥KP').
Az αβγ▵ oldala nem lehet nagyobb az ω1ω2 távolság kétszeresénél.
Faragó Andor
1Az egyenlő oldalú háromszögbe írt tetszőleges háromszög bármely oldala kisebb az egyenlő oldalú háromszög oldalánál.

2L. még részletesebben e szerkesztést és taglalását a XII. évf. 1. számában, 21. o.

1L. az 1. sz.-ban, a tanulmányi verseny II. feladatát.