Kezdőlap


Feladat:	1246. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Herczeg Gy. , Komlós J. , Lóránd E. , Schwarz J.
Füzet:	1936/november, 83 - 84. oldal		PDF \| MathML
Témakör(ök):	Merőleges affinitás, Kúpszeletek érintői, Paralelogrammák, Téglalapok, Síkgeometriai szerkesztések, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1936/szeptember: 1246. matematika feladat

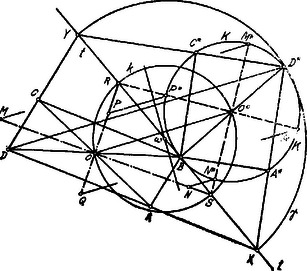
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ellipszis $O$ középpontjára nézve $A$ -val szimmetrikus $C$ és $B$ -vel szimmetrikus $D$ szintén az ellipszis pontjai. Az $A B C D$ idom, melynek átlói felezik egymást, paralelogramma; ennek az affin körben szintén paralelogramma,^{$^{*}$} tehát téglalap felel meg: a $B A D ∢$ -nek $90^{\circ}$ -ú szög.

t

érintője lesz az affin körnek, ugyancsak a

B

pontban.^{$^{*}$} Ezért az affin kör középpontja a

B

pontban

t

-re állított merőlegesen lesz. Az

A D

C D

egyenesek a

t

-t az

X

Y

pontokban metszik; ezekben metszik

t

-t az

A D

és

A C

affin egyenesei is, amelyeknek az előbbiek szerint egymásra merőlegeseknek kell lenniök, tehát metszéspontjuk,

D^{*}

, az

X Y

átmérő felett szerkesztett

γ

félkörön fekszik. Az ellipszis

B D

átmérőjének megfelelő kör-átmérő ugyancsak

B

-ből indul ki: tehát a

B

pontban,

t

-re állított merőleges a

γ

félkört a

D^{*}

pontban metszi.
Eszerint

B D^{*}

az affin kör átmérője, helyzet és nagyság szerint; felezőpontja

O^{*}

a kör középpontja. Legyen ezen kör

K

.
A

D^{*}

meghatározza a

K

körben az

A^{*} B C^{*} D^{*}

téglalapot, az

A B C D

-nek megfelelő idomot. Az affinitás iránya pl.

D^{*} D

.
Az ellipszis főtengelyei (mint konjugált átmérők) a kör oly két átmérőjének felelnek meg, amelyek egymásra merőlegesek. A főtengelyek és az affin kör-átmérők az affinitás-tengelyét ugyanazon pontokban metszik. A főtengelyek által alkotott derékszög csúcsa,

O

és az affin kör-átmérők derékszögének csúcsa

O^{*}

egy oly

k

kör pontjai, melynek átmérője a

t

-n fekszik. Ezen kör

O O^{* *}

húrját felező egyenes a

t

-t a

k

kör

ω

középpontjában metszi, és a

k

t

-n az

R S

átmérőt határozza meg.

O R

és

O S

egyenesek lesznek a főtengelyek tartói. A főtengelyeknek megfelelő körátmérők

P^{*} O^{*} Q^{*}

és

M^{*} O^{*} N^{*}

(az

O^{*} R

és

O^{*} S

egyeneseken feküsznek). A

P^{*}

-ből ill.

N^{*}

-ből

D^{*} D

-vel párhuzamosan vont egyenes

O R

-en a

P

ill.

O S

-n az

N

pontot határozzák meg, úgy hogy

P O Q

és

N O M

az ellipszis főtengelyei lesznek.

^{$^{*}$}Párhuzamos egyeneseknek párhuzamos egyenesek felelnek meg az affinitásban (L. XI.-évf. 241. o.)

^{$^{*}$}Az affinitás tengelyén fekvő pontok önmaguknak felelnek meg. Érintőnek érintő felel meg. (L. ugyanott)