Kezdőlap


Feladat:	1245. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barna T. , Bodó Zalán , Czinczenheim J. , Donáth G. , Farkas I. , Huhn Péter , Kardos Gy. , Kernáts A. , Komlós J. , Lóránd E. , Nagy E. , Pálos P. , Polónyi J. , Schwarz J.
Füzet:	1936/november, 82 - 83. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Szögfelező egyenes, Beírt kör, Hozzáírt körök, Kör (és részhalmaza), mint mértani hely, Húrnégyszögek, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1936/szeptember: 1245. matematika feladat

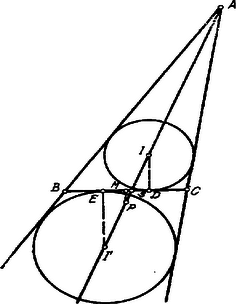
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. a) Az $A$ csúcs az $(I)$ és $(I')$ körök külső hasonlósági pontja.

Ha e körök sugarai

r

és

r_{a}

, akkor az

A

pontra nézve

\begin{matrix} \frac{A I}{A I'} = \frac{r}{r_{a}} = \frac{p}{q} . \end{matrix}

Eszerint az

A

pont helyzete az

I I'

centrális egyenesen meg van határozva.
b) A

B C

oldal a szóban forgó két kör egyik közös belső érintője; ez azonban mindig a két kör belső hasonlósági pontján, az

I I'

centrális

S

pontján megy keresztül. Az

S

pontra nézve

\begin{matrix} \frac{S I}{S I'} = - \frac{r}{r_{a}} = - \frac{p}{q}, \end{matrix}

tehát az

S

pont az

I I'

egyenesnek egy szilárd pontja.^{$^{*}$}
c) Az

(I)

kör érintési pontja a

B C

oldalon legyen

D

, az

(I')

köré

E

; ekkor

B E = C D

és ezért a

B C

oldal felezőpontja,

M

összeesik a

D E

távolság felezőpontjával. Ez azonban az

I I'

távolság felezőpontjának,

P

-nek vetülete a

B C

egyenesen. Ebből következik, hogy az

M

pont mértani helye a

P S

átmérő felett szerkesztett kör.

Huhn Péter (Kegyesrendi g. VIII. o. Szeged.)

II. Megoldás.

3^{0}

I B

és

I' B

A B C ▵

B

csúcsához tartozó belső- és külső szögfelezők egymásra merőlegesek. Hasonlóan

I C ⊥ I' C

. Ezért az

I B I' C

idom húrnégyszög az

I I'

átmérőjű körben, melynek középpontja

P

. Ezen körnek változó húrja

B C

, mely azonban az

S

szilárd ponton megy keresztül. Egy szilárd

S

ponton átmenő húrok felezőpontjainak mértani helye oly kör, melynek átmérője

S P

Bodó Zalán (Szent István rg. VII. o. Bp. VII.)

^{$^{*}$}

(I, I')

és

(S, A)

harmonikus pontpárok.