Kezdőlap


Feladat:	1231. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	B. Major Pál , Barna T. , Czinczenheim J. , Datner P. , Farkas I. , Gilyén J. , Illovszky G. , Kálmán L. , Kardos Gy. , Kukorelly Gy. , Lóránd E. , Nagy Ernő , Nemes F. , Pálos P. , Schmitterer J. , Schwarz J.
Füzet:	1936/október, 45 - 48. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Másodfokú (és arra visszavezethető) egyenletek, Fizikai jellegű feladatok, Derékszögű háromszögek geometriája, Egyenes körkúpok, Terület, felszín, Térfogat, Gömb és részei, Fotometria, Árnyékjelenségek, Feladat
Hivatkozás(ok):	Feladatok: 1936/május: 1231. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen ‐ ábránk szerint ‐ 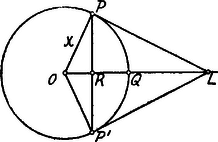$L O = 1$ ; $O P = O Q = x$ .

Minthogy az

O P L

derékszögű háromszögben az

O P

befogó vetülete az átfogón

O R

\begin{matrix} {\bar{O P}}^{2} = \bar{O L} \cdot \bar{O R}, azaz O R = x^{2} . \end{matrix}

Így

Q R = x - x^{2}

és

P R = \sqrt[]{x^{2} - x^{4}} = x \sqrt[]{1 - x^{2}}

a)

A gömbsüveg felszíne az

f = 2 r π m

alapján, minthogy

r = x

és

m = Q R = x - x^{2}

\begin{matrix} f = 2 π x (x - x^{2}) = 2 π (x^{2} - x^{3}) . \end{matrix}

Vizsgálnunk kell az

y = x^{2} - x^{3}

függvényt 0 és 1 között.

y = 0

, ha

x = 0

és ha

x = 1

. Ezen közben mindenütt folytonos és pozitív. Kell tehát, hogy ezen közben legalább egy maximuma legyen, mégpedig ott, ahol

\begin{matrix} y' = 2 x - 3 x^{2} = x (2 - 3 x) = 0, tehát x = 0 vagy x = \frac{2}{3} . \end{matrix}

x = 0

helyen

y'

negatív értékekből megy át pozitívokba. Itt minimum van.

x = \frac{2}{3}

helyen

y'

pozitív értékekből megy át negatívokba. Itt maximum van.

b)

t = {\bar{P R}}^{2} \cdot π = (x^{2} - x^{4}) π

. Itt ez

y = x^{2} - x^{4}

függvényről ugyanazt mondhatjuk, mint

a)

alatt.

\begin{matrix} y' = 2 x - 4 x^{3} = 2 x (1 - 2 x^{2}) = 0, ha x = 0 vagy x = \frac{\sqrt[]{2}}{2} .^{1} \end{matrix}

¹ Maximum van az

x = \frac{\sqrt[]{2}}{2}

helyen.

\begin{matrix} c) f + t = 2 π (x^{2} - x^{3}) + π (x^{2} - x^{4}) = π (3 x^{2} - 2 x^{3} - x^{4}) . \end{matrix}

y = 3 x^{2} - 2 x^{3} - x^{4}

függvényről ugyanazt mondhatjuk, mint az előbbi esetekben. (Az összeg mindegyik tagja megegyező módon viselkedik.)

\begin{matrix} y' = 6 x - 6 x^{2} - 4 x^{3} = 2 x (3 - 3 x - 2 x^{2}) = 0, \end{matrix}

\begin{matrix} x = 0 és ha 3 - 3 x - 2 x^{2} = 0. \end{matrix}

x = 0

helyen minimum van. Továbbá

2 x^{2} + 3 x - 3 = 0

,
ha

\begin{matrix} x = \frac{- 3 \pm \sqrt[]{9 + 24}}{4} . \end{matrix}

(0, 1)

intervallumban csak

x = \frac{\sqrt[]{33} - 3}{4} \approx 0.686

helyen van maximum.

d)

A szóban forgó kúppalást felszíne

\begin{matrix} p = π \cdot O P \cdot P R = π x \cdot x \sqrt[]{l - x^{2}} = π x^{2} \sqrt[]{1 - x^{2}} . \end{matrix}

Itt az

x^{2} \sqrt[]{1 - x^{2}}

helyett vizsgálhatjuk a négyzetét, azaz

\begin{matrix} y = x^{4} (1 - x^{2}) = x^{4} - x^{6} \end{matrix}

függvény változását. A

(0, 1)

intervallumban ez is folytonos és mindenütt pozitív, a határhelyeken

0

. Kell tehát, hogy a jelzett közben legalább egy maximuma legyen, még pedig ott, ahol

\begin{matrix} y' = 4 x^{3} - 6 x^{5} = 2 x^{3} (2 - 3 x^{2}) = 0. \end{matrix}

A jelzett közben csak a

2 - 3 x^{2} = 0

pozitív gyöke van:

x = \sqrt[]{\frac{2}{3}} \approx 0.8165

e)

A gömbszelet köbtartalma

\begin{matrix} k_{1} = \frac{π}{3} {\bar{Q R}}^{2} (3 O Q - Q R) = \frac{π}{3} {(x - x^{2})}^{2} (2 x + x^{2}) . \end{matrix}

y = {(x - x^{2})}^{2} (2 x + x^{2})

függvénye a

(0, 1)

intervallumban mindenütt folytonos és pozitív, a határhelyeken

0

. Kell tehát, hogy a jelzett közben legalább egy maximuma legyen.

\begin{matrix} y = {(x - x^{2})}^{2} (2 x + x^{2}) = 2 x^{3} - 3 x^{4} + x^{6}, \\ y' = 6 x^{5} - 12 x^{3} + 6 x^{2} = 6 x^{2} (x^{3} - 2 x + 1) = 6 x^{2} (x - 1) (x^{2} + x - 1) . \end{matrix}

y'

eltűnik az

x = 0

x = 1

helyeken, továbbá ott, ahol

\begin{matrix} x^{2} + x - 1 = 0 azaz x = \frac{- 1 \pm \sqrt[]{5}}{2} . \end{matrix}

A jelzett közben csak

x = \frac{- 1 + \sqrt[]{5}}{2}

helyezkedik el. Itt tehát

k_{1}

-nek maximuma van.
NB.

x

O L = 1

távolságot az aranymetszés szerint osztja két részre.

f)

d)

alatti kúp köbtartalma

\begin{matrix} k_{2} = \frac{π}{3} \cdot {\bar{P R}}^{2} \cdot \bar{O R} = \frac{π}{3} (x^{2} - x^{4}) \cdot x^{2} = \frac{π}{3} (x^{4} - x^{6}) . \end{matrix}

y = x^{4} - x^{6} = x^{4} (1 - x^{2})

függvénynek, mely az előbbiekhez hasonló módon viselkedik a (0, 1) közben, maximuma ott van, ahol

\begin{matrix} y' = 4 x^{3} - 6 x^{5} = 3 x^{2} (2 - 3 x^{3}) = 0. \end{matrix}

Itt ismét csak az

x = \sqrt[]{\frac{2}{3}}

helyen van a függvénynek, ill.

k_{2}

-nek maximuma (L. (d) alatt).

g)

A gömbcikk köbtartalma felírható

k_{1} + k_{2}

alakban:

\begin{matrix} k_{1} + k_{2} = \frac{π}{3} (2 x^{3} - 3 x^{4} + x^{6}) + \frac{π}{3} (x^{4} - x^{6}) = \frac{2 π}{3} (x^{3} - x^{4}) . \end{matrix}

y = x^{3} - x^{4}

függvény differenciálhányadosa

\begin{matrix} y' = 3 x^{2} - 4 x^{3} = x^{2} (3 - 4 x) . \end{matrix}

Minthogy

y

a (0, 1) intervallumban folytonos és pozitív, a határhelyeken zérus, maximuma van, ha

\begin{matrix} 3 - 4 x = 0, azaz ha x = \frac{3}{4} . \end{matrix}

B. Major Pál (ref. rg. VII. o. Csurgó.)

- \frac{\sqrt[]{2}}{2}

nincs a vizsgált intervallumban.