Kezdőlap


Feladat:	1225. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Czinczenheim J. , Datner P. , Erdős G. , Gárdos P. , Gergely J. , Kolostori J. , Komlós J. , Lóránd E. , Polányi J.
Füzet:	1936/szeptember, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Merőleges affinitás, Kúpszeletek érintői, Síkgeometriai szerkesztések, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1936/április: 1225. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adatok alapján meg tudjuk szerkeszteni az ellipszis két konjugált átmérőjét irány és nagyság szerint, az affinitás segítségével. Ennek egyik módja a következő: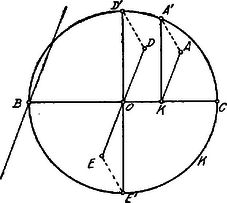
Legyen $B$ -nek az $O$ -ra nézve szimmetrikusa $C$ ; ekkor $B C$ az ellipszis átmérője és ezt válasszuk az affinitás tengelyéül. Az ellipszist abból a $k$ körből kapjuk affin transzformációval, amelynek átmérője $B C$ . Meg kell határoznunk az affinitás irányát.

B C

-vel konjugált átmérő iránya megegyezik a

t

érintő irányával; a konjugált átmérő az

O

ponton megy keresztül és nem egyéb, mint a

B C

-re merőleges

D' C'

körátmérő valamely parallel‐vetülete.¹ Hogy a vetítő‐sugár (ill. affinitás) irányát megkapjuk, megállapítjuk, hogy az

A

pont a

k

kör mely pontjának transzformációja? Húzzunk tehát az

A

pontból

t

-vel párhuzamost; messe ez

B C

-t a

K

pontban; a

K

pontba

B C

-re állított merőleges a

k

kört azon

A'

pontban metszi, amelynek affin pontja

A

. Eszerint

A' A

az affinitás iránya.
A

D'

ill.

E'

pontból az

A' A

-val vont párhuzamos meghatározza a

B C

-vel konjugált átmérő

D

ill.

E

végpontját azon egyenesen, amely

O

-n keresztül

t

-vel párhuzamosan halad.
Már most a konjugált átmérők egy párja adva lévén, irány és nagyság szerint meg kell szerkesztenünk az ellipszis főtengelyeit.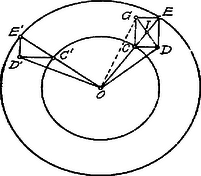

Legyen tehát a konjugált félátmérők párja

O D

és

O D'

; tegyük fel továbbá, hogy feladatunkat megoldva,

O C = b

és

O E = a

sugarakkal koncentrikus köröket szerkesztünk az

O

-körül,

a

ill.

b

a nagy- ill. kistengely felét jelenti.

C D

E D

a főtengelyekkel párhuzamosak, azaz

D

E

pont affintranszformációja (a főtengelyre vonatkoztatva). Ekkor

D'

O E

-re merőleges

O E'

sugár

E'

végpontjának affin képe. Már most

C' D' E' ▵ ≅ E D C ▵

, mert

C' E' = C E

és szögeik egyenlők. Ebből következik:

E' D' = C D

.
Forgassuk az

E' D' O ▵

-et

90^{\circ}

-kal

O

körül. Az

E'

pont az

E

-be,

D'

G

pontba kerül, úgy hogy

G E = D' E'

, tehát

G E # C D

. Eszerint a

C D E G

idom téglalap, melynek átlói az

I

pontban felezik egymást.
Ezek alapján a főtengelyek szerkesztése a következőképpen történik: az

O D'

-re az

O

pontban merőlegest állítunk és erre rámérjük az

O G = O D'

távolságot. A

D G

távolság

I

felezőpontját összekötjük

O

-val és ezen egyenesen felmérjük az

I E = I C = \frac{D G}{2}

távolságot.

O C

az ellipszis kis,

O E

a nagytengely fele lesz. A nagytengely

C D

-vel lesz párhuzamos.

Jegyzet:

1^{\circ}

. Az affinitás tengelyéül választhatjuk az

O A

-t is, vagy pedig a

t

érintőt is. Az utóbbi móddal kapcsolatban még egyszer kitűzzük a feladatot.

2^{\circ}

. Az ellipszis konjugált átmérőinek ismerete alapján a főtengelyek megszerkesztése többféle módon lehetséges. A közölt eljárás, egyike a legegyszerűbbeknek, Mannheim Amadäus-tól való. (A párisi École Polytechnique tanára volt.)
Egy másik, ugyancsak könnyen áttekinthető szerkesztés kedvéért az ellipszisre vonatkozólag néhány tételt fogunk kitűzni.

¹Az ellipszis konjugált átmérői a kör két egymásra merőleges átmérőjének transzformációjából keletkeznek.