Kezdőlap


Feladat:	1223. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Barna T. , Földesi T. , Gárdos P. , Gergely J. , Kardos Gy. , Nagy Elemér , Nagy Ernő , Nemes F. , Pálos Pelegrin , Radovics Gy. , Varga Tamás
Füzet:	1936/szeptember, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Szöveges feladatok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1936/április: 1223. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje $O$ a Föld középpontját, $A$ a magasabb, $B$ az alacsonyabb hegy csúcsát. $O A$ a Föld felületét $C$ -ben, $O B$ pedig $D$ -ben metszi úgy, hogy $C D$ a Föld egyik legnagyobb körének íve, $A C$ , ill. $B D$ a hegymagasság. $(A C = 8800$ m, $B D = 7050$ m.) Az $A$ pontból a $C D$ körhöz húzott érintő $C D$ -t az $E$ pontban érinti, $B D$ -t a $B'$ pontban metszi. A $B$ pontból a $C D$ -hez húzott érintő $C D$ -t az $F$ pontban érinti, $A C$ -t az $A'$ pontban metszi. Az $A$ csúcsról a másik hegyből $B B'$ , a $B$ csúcsról a másik hegyből $A A'$ magasságú rész látható.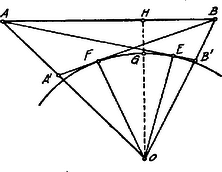

a) Már most

\begin{matrix} B B' = O D + D B - O B' = 6366 + 7, 05 - O B' = 6373, 05 - O B' . \\ A A' = O C + C A - O A' = 6366 + 8, 8 - O A' = 6374, 8 - O A' . \end{matrix}

A O B' ▵

-ben adva van: az

A O

oldal, az

O E

magasság és az

A O B ∢ = α = 4^{\circ} 30'

\begin{matrix} A O = A C + C O = 8, 8 + 6366 = 6374, 8 km . \end{matrix}

O E = 6366

km. Kiszámíthatjuk először az

A O E ∢

-et.

\begin{matrix} cos A O E = \frac{O E}{A O} = \frac{6366}{6374, 8} és így A O E ∢ = 3^{\circ} . Ezért E O B' ∢ = 1^{\circ} 30' . \end{matrix}

E O B' ▵

-ből

\begin{matrix} O B' = \frac{O E}{cos 1^{\circ} 30'} = \frac{6366}{cos 1^{\circ} 30'} = 6368, 4 km . \end{matrix}

Eszerint

\begin{matrix} B B' = 6373, 05 - 6368, 4 = 4, 65 km = 4650 m . \end{matrix}

Hasonlóan a

B O A' ▵

-ben ismeretes: a

B O

oldal, az

O F

magasság, a

B O A' ∢ = 4^{\circ} 30'

. Kiszámítjuk a

B O F ∢

-et; t. i.

\begin{matrix} cos B O F = \frac{O F}{B O} = \frac{6368}{6373, 05}; innen B O F ∢ = 2^{\circ} 40' \end{matrix}

és így

\begin{matrix} F O A' ∢ = 4^{\circ} 30' - 2^{\circ} 40' = 1^{\circ} 50' . \end{matrix}

F O A ▵

-ből

\begin{matrix} O A' = \frac{O F}{cos 1^{\circ} 50'} = \frac{6366}{cos 1^{\circ} 50'} = 6369, 3 km . \end{matrix}

Tehát

A A' = 6374, 8 - 6369, 3 = 5, 5 km = 5500 m

.
b) Az

A O B ▵

magassága, az

A B

oldalra vonatkoztatva

O H

; ez a

C D

kört a

G

pontban metszi.

G H

jelenti az

A B

egyenesnek a

C D

-től való legkisebb távolságát

G H = O H - O G = O H - 6366

.
Ki kell számítanunk az

O H

-t. Az

A O B ▵

területe alapján:

\begin{matrix} A B \cdot O H = A O \cdot B O \cdot sin A O B és így O H = \frac{6374, 8 \cdot 6373, 05 \cdot sin 4^{\circ} 30'}{A B} . \end{matrix}

A cosinus‐tétel alapján

\begin{matrix} A B = {({\bar{A O}}^{2} + {\bar{B O}}^{2} - 2 \bar{A O} \cdot \bar{B O} cos \hat{A O B})}^{\frac{1}{2}} = 500, 5 km . \end{matrix}

A B

ezen értékével

O H = 6368, 7

km és

G H = 2, 7 km = 2700 m