| Feladat: | 1212. matematika feladat | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Abonyi Péter , Barna T. , Brill Gy , Bukszbaum Gy. , Czinczenheim J. , Faragó P. , Farkas I. , Földesi T. , Gergely J. , Glück P. , Grózinger S. , Gyulai L. , Huhn P. , ifj. Csizmás L. , Ilkovits I. , Kádár Gy. , Kapcsándi I. , Kardos Gy. , Keller Vera , Kepes Á. , Kerényi R. , Kolostori J. , Komlós J. , Kukorelly Gy. , Lóránd E. , Major P. , Mandl B. , Mérei Gy. , Molnár F. , Nagy Elemér , Nagy Ernő , Nemes F. , Oroszhegyi Szabó Lajos. , Pálos P. , Pázmándi L. , Pick Gy. , Sájerman J. , Schreiber B. , Schwarz J. , Schwarz O. , Somogyi Éva , Szak Á. , Szél György , Szele T. , Szelei Gy. , Zalay E. | ||
| Füzet: | 1936/május, 259 - 260. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Merőleges affinitás, Ellipszis egyenlete, Síkbeli ponthalmazok távolsága, Síkgeometriai szerkesztések, Ellipszis, mint mértani hely, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1936/március: 1212. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Megoldás. . Az ellipszisnek a főtengelyekre vonatkoztatott egyenlete: Tekintsük azon gyújtópontot, mely az -tengely pozitív oldalán van. Olyan pont, mely az ellipszis középpontjától és az gyújtóponttól egyenlő távolságban van, kettő fekszik az ellipszisen, az -tengelyre nézve szimmetrikusan. Elegendő tehát, ha csak azt vesszük figyelembe, amelyre nézve . A szóban forgó pontot az abscissa határozza meg, ahol . Ezen abscissához tartozó pont ordinátája 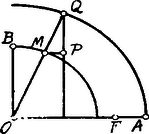 . A pont szerkesztése az affinitás alapján végezhető. Az ellipszis főkörét az egyenes a (ill. ezzel szimmetrikus ) pontban metszi. Az egyenes az körül sugárral szerkesztett kört pontban metszi. Az pontból az -tengellyel párhuzamosan vont egyenes az egyenesen a keresett pontot határozza meg.
II. Megoldás. Azon körök középpontjainak mértani helye, amelyek egy adott kört érintenek és egy, a körön belül fekvő ponton mennek keresztül, ellipszis. Ennek gyújtópontjai az adott kör középpontja, , és az adott pont ; nagytengelye az adott kör sugara. Ebből következik, hogy az ellipszis bármely pontja egyenlő távolságban van az gyújtóponttól és az középpontból sugárral rajzolt ellenkörtől, azaz oly kör középpontja, mely keresztülmegy -n és a kört érinti. Már most az ellipszis pontját úgy kell megkeresnünk, hogy oly kör középpontja legyen, mely az előbbi feltételek mellett még az ellipszis középpontján menjen keresztül. 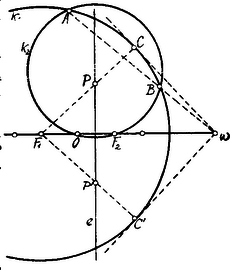 Vegyünk fel tehát egy tetszőleges kört, mely keresztülmegy az és pontokon és a kört az , pontokban metszi. A keresett kör legyen . A és hatványvonala az egyenes, és hatványvonala az egyenes. Az és metszéspontja legyen : ezen kell áthaladnia a és hatványvonalának is. Minthogy ezen két kör érinti egymást, hatványvonaluk a közös érintőjük: tehát az -ból -hez húzott érintő ill. . Ha tehát -t és -t összekötjük középpontjával, -vel, megkapjuk az -t merőlegesen felező egyenesen az ellipszis keresett pontjait, -t és -t.
|