Kezdőlap


Feladat:	1203. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barabás J. , Bodó Z. , Erdős G. , Farkas I. , Finszter L. , Gergely J. , Harsányi J. , Huhn P. , ifj. Csizmás Lajos , Ilkovits I. , Kádár Gy. , Kardos Gy. , Kerekes Katalin , Kolostori J. , Komlós J. , Kukorelly Gy. , Morvay S. , Nádas B. , Nagy Elemér , Nagy Ernő , Nagy J. , Oroszhegyi Szabó Lajos. , Pálos P. , Papp Gy. , Pázmándi L. , Schwarz J. , Szele T.
Füzet:	1936/április, 242 - 243. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Beírt kör középpontja, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1936/február: 1203. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen valamely $P$ pont az $A_{1} B_{1} C_{1} Δ$ -ön belül. Az $A P$ , $B P$ , $C P$ egyenesek a $B C$ , $C A$ , $A B$ oldalakat az $A'$ , $B'$ , $C'$ pontokban messék.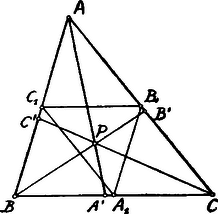

Akkor (mivel

B_{1} C_{1}

felezi

A A'

-t),

\begin{matrix} A P > A' P, B P > B' P, C P > C' P . \end{matrix}

Viszont, ha ezen feltételek egyszerre fennállanak, akkor a

P

pont az

A_{1} B_{1} C_{1} Δ

-ön belül fekszik.
Ha már most

P \equiv O

, ahol

O

A B C_{Δ}

-be írt kör középpontja, akkor

A P

felezi az

A ∢

-et,

C P

felezi a

C ∢

-t, tehát

\begin{matrix} \frac{C P}{C' P} = \frac{A C}{A C'} = \frac{B C}{B C'} = \frac{A C + B C}{A B} > 1. \end{matrix}

Hasonlóan:

\begin{matrix} \frac{A P}{A' P} > 1 és \frac{B P}{B' P} > 1. \end{matrix}

Eszerint a

P \equiv O

pont az

A_{1} B_{1} C_{1} Δ

-ön belül esik.

II. Megoldás. A beírt kör középpontja az

A_{1} B_{1} C_{1} Δ

-ön belül esik, ha a beírt kör sugara bármelyik magasság felénél kisebb.
Hasonlítsuk össze tehát a beírt kör sugarát pl. az

a

oldalhoz tartozó magasság felével.
A beírt kör sugara

ϱ = \frac{t}{s}

, ahol

t

a háromszög területe, míg

\begin{matrix} s = \frac{1}{2} (a + b + c) . \end{matrix}

a

oldalhoz tartozó magasság

m_{1} = \frac{2 t}{a}

és ennek fele

\frac{t}{a}

.

Azonban:

\begin{matrix} b + c > a, tehát 2 s = a + b + c > 2 a \end{matrix}

és így

s > a

.

Ezért

\begin{matrix} \frac{t}{s} < \frac{t}{a}, azaz ϱ < \frac{m_{1}}{2} . \end{matrix}

Hasonlóan:

\begin{matrix} ϱ < \frac{m_{2}}{2} és ϱ < \frac{m_{3}}{2} . \end{matrix}

ifj. Csizmás Lajos (Árpád vezér rg. VIII. o. Bp. III.)