Kezdőlap


Feladat:	1199. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	B. Major P. , Bodó Z. , Brill Gy. , Bukszbaum Gy. , Czinczenheim J. , Eggenhoffer Gy. , Fábián J. , Farkas I. , Földesi T. , Gergely J. , Groág J. , Harsányi J. , Herczeg Gy. , Huhn P. , Ilkovits I. , Jacoby Gy. , Kapcsándi I. , Kardos Gy. , Keller Vera , Kepes Á. , Kerényi R. , Kolostori Gy. , Komlós János , Kukorelly Gy. , Lóránd E. , Mezei Gy. , Molnár F. , Müller S. , Nagy Elemér , Nagy Ernő , Oroszhegyi Szabó Lajos. , Pálos P. , Papp J. , Pázmándi L. , Pick Gy. , Schwarz J. , Schwarz O. , Sebestyén Gy. , Szak Á. , Szele T. , Szelei Gy. , Szmák Z. , Szűcsi I. , Tarnóczy L. , Vajda J. , Vezekényi A. , Zalay E.
Füzet:	1936/április, 239 - 240. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1936/február: 1199. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott egyenesek egyenleteit:

\begin{matrix} \frac{a x}{b c} + \frac{y}{c} = 1, & (1) \\ \frac{a x}{b c} + \frac{y}{b} = 1, & (2) \\ \frac{x}{a} + \frac{y}{b} = 1, & (3) \\ \frac{x}{a} + \frac{y}{c} = 1 & (4) \end{matrix}

alakban írva, nyilvánvaló, hogy az (1) és (2) egyenesek az

X

-tengely ugyanazon

M

pontján

(x = \frac{b c}{a}, y = 0)

mennek keresztül, továbbá a (3) és (4) egyenesek is az

X

-tengely valamely

N

pontján

(x = a, y = 0)

mennek keresztül. Másrészt: az (1) és (2) egyenesek az

Y

tengelyen ugyanazon szeletet metszik, mint a (3) és (4) egyenesek, t. i.

y = b

és

y = c

(de

x = 0

) koordinátákhoz tartozó pontok közötti szeletet (

B C

-t).
Az egyenesek irányhatározói rendre:

\begin{matrix} ... - \frac{a}{b}, & (1) \\ ... - \frac{a}{c}, & (2) \\ ... - \frac{b}{a}, & (3) \\ ... - \frac{c}{a} . & (4) \end{matrix}

Az (1) és (2) egyenesek hajlásszögére nézve:

\begin{matrix} tg α_{1,2} = \pm \frac{- \frac{a}{b} + \frac{a}{c}}{1 + \frac{a^{2}}{b c}} = \pm \frac{- a c + a b}{b c + a^{2}} . \end{matrix}

A (3) és (4) egyenesek hajlásszögére nézve:

\begin{matrix} tg α_{3,4} = \pm \frac{- \frac{b}{a} + \frac{c}{a}}{1 + \frac{b c}{a^{2}}} = \pm \frac{- a b + a c}{a^{2} + b c} . \end{matrix}

Ezen hajlásszögek tangenseit azért kell

\pm

előjellel vennünk, mert

b

és

c

értékekre nézve nincsenek közelebbi adataink és így nem tudjuk, hogy a pozitív forgás irányában az (1) egyenestől jutunk-e a (2)-höz vagy (2)-től az (1)-hez, ill. (3)-tól a (4)-hez vagy (4)-től a (3)-hoz?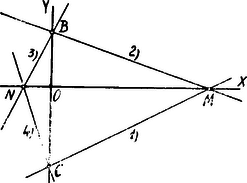

Mindenesetre áll: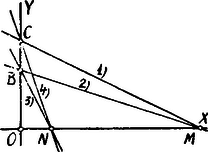

\begin{matrix} tg α_{1,2} = \pm tgα_{3,4} \end{matrix}

azaz vagy

\begin{matrix} α_{1,2} = α_{3,4} vagyα_{1,2}+α_{3,4}=180^{\circ}. \end{matrix}

α_{1,2} = α_{3,4}

, ha

b

és

c

megegyező előjelűek; ekkor

\frac{b c}{a}

és

a

is megegyező előjelűek, az

M

és

N

pontok az

X

-tengely ugyanazon felén feküsznek.

α_{1,2} + α_{3,4} = 180^{\circ}

, ha

b

és

c

ellenkező előjelűek; ekkor

\frac{b c}{a}

és

a

ellenkező előjelűek, az

M

és

N

pontok az

X

-tengely ellenkező felén feküsznek.

Mind a két esetben az

M

N

pontok, továbbá a

B (x = 0, y = b)

és

C (x = 0, y = c)

pontok húrnégyszög csúcsai.
Az első esetben azért, mert a

B C

távolság az

M

és

N

pontokból egyenlő szögek alatt látható; a második esetben pedig azért, mert a

B C

távolság az

M

és

N

pontokból kiegészítő szögek alatt látható.

II. Megoldás. Az M, N, B, C pontokon átmenő kör egyenletét állapították meg: Brill Gy., Farkas L. Fábián J. És Jacoby Gy., Földesi T., Groág J., Sebestlyén J., Kolostori Gy., Kukorelly Gy., Müller S., Papp j., Pick Gy., Schwarz J., Sebestyén J., Szelei Gy., Szűcs L., Vajda J., Tarnóczy J.

III. Megoldás. Az MNBC négyszögre a Ptolemaus-tétel érvényességét mutatták ki: Keller Vera, Mezei Gy.

Jegyzet. Könnyen igazolható, hogy

O M \cdot O N = O B \cdot O C = b c

, azaz az

M

N

B

C

pontok egy körön feküsznek.
Ha

b c > 0

, akkor az

O

pontnak a körre vonatkozó hatványa pozitív, tehát az

O

pont a körön kívül, ha

b c < 0

, akkor az

O

pont a körön belül fekszik (a körre vonatkozó hatványa negatív).