Kezdőlap


Feladat:	1198. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Barabás J. , Barna T. , Bencze J. , Brucker I. , Datner P. , Fábián J. , Faragó P. , Farkas I. , Fleischer Gy. , Gergely J. , Gyulai L. , Herczeg Gyula , Huhn P. , ifj. Csizmás L. , Jacoby Gy. , Kádár Gy. , Kapcsándi I. , Kardos Gy. , Keller Vera , Kepes Á. , Kerekes Katalin , Kerényi R. , Kolostori Gy. , Komlós J. , Lóránd E. , Mandl B. , Mezei Gy. , Nagy Elemér , Nagy Ernő , Nagy J. , Nemes F. , Oroszhegyi Szabó Lajos. , Pálos P. , Pázmándi L. , Pick Gy. , Radovics Gy. , Sájermann I. , Scheiber J. , Schmitterer J. , Schwarz J. , Seidl G. , Somogyi Éva , Sorok J. , Szabó László , Szak Á. , Szél Gy. (Kölcsey) , Szele T. , Szelei Gy. , Szűcsi I. , Tarnóczy L. , Vajda J. , Veress N. , Vezekényi A. , Villani F. , Zalay E.
Füzet:	1936/április, 237 - 238. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Egyenlő szárú háromszögek geometriája, Hossz, kerület, Terület, felszín, Húrnégyszögek, Mértani sorozat, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1936/február: 1198. matematika feladat

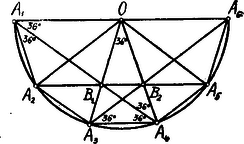
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rajzoljunk meg a szabályos tízszögből annyit, amennyi a rákövetkező tízszög egy oldalának kialakításához szükséges, tehát az $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ , $A_{5}$ , $A_{6}$ csúcspontok közé eső oldalakat.

A_{1} A_{4}

A_{2} A_{5}

A_{3} A_{6} ...

átlók felezik a szabályos tízszög szögeit. Ugyanis pl. az

A_{1} A_{2} A_{3} A_{4}

húrnégyszögben

A_{1} A_{2} A_{3} ∢ = 144^{0}

, tehát a vele szemben fekvő szög

\begin{matrix} A_{1} A_{4} A_{3} ∢ = 180^{\circ} - 144^{\circ} = 36^{\circ}^{1} . \end{matrix}

¹ Az

A_{1} A_{4}

átló

O A_{3}

-t a

B_{1}

A_{3} A_{6}

átló

O A_{4}

-t a

B_{2}

pontban metszi. Minthogy

A_{3} A_{6}

és

A_{4} A_{1}

-t az

O A_{3} A_{4}

egyenlő szárú háromszög tengelyére nézve szimmetrikus egyenesek

A_{3} B_{1} = A_{4} B_{2}

. Hasonlóan kell, hogy az

A_{2} A_{5}

átló az

O A_{3}

-t a

B_{1}

O A_{4}

-t a

B_{2}

pontban messe. Eszerint a három átló létrehozza

B_{1} B_{2}

-t. mint az új tízszög oldalát.
Az

O A_{3} B_{2} Δ

-ben az

O A_{3}

oldalon fekvő szögek mindegyike

36^{\circ}

, ebből következik:

A_{3} B_{2} = O B_{2}

. Továbbá

A_{4} A_{3} B_{2} Δ

is egyenlőszárú:

A_{3} B_{2} = A_{3} A_{4} = a_{10}

. Eszerint

O B_{2} = a_{10}

^{$^{*}$} azaz az új tízszög köré írt kör sugara megegyezik az első tízszög oldalával.
Minthogy

a_{10} = \frac{r}{2} (\sqrt[]{5} - 1)

, az új tízszög oldala:

B_{1} B_{2} = \frac{a_{10}}{2} (\sqrt[]{5} - 1)

Hasonlóan a

B_{1} B_{2} B_{3} ...

sokszögben az átlók megfelelő módon való szerkesztése után keletkező új tízszög oldala:

\begin{matrix} C_{1} C_{2} = \frac{B_{1} B_{2}}{2} (\sqrt[]{5} - 1) = a_{10} \cdot {(\frac{\sqrt[]{5} - 1}{2})}^{2} s. i. t . \end{matrix}

Eszerint a sorban keletkező szabályos tízszögek oldalai, illetve kerületei oly mértani sort alkotnak, melynek hányadosa:

0 < \frac{\sqrt[]{5} - 1}{2} < 1

. A végtelen sor tehát összetartó és így a végtelen sok tízszög kerületének összege, ha az első

k_{10}

\begin{matrix} s = k_{10} \frac{1}{1 - \frac{\sqrt[]{5} - 1}{2}} = k_{10} \frac{2}{3 - \sqrt[]{5}} = k_{10} \frac{2 (3 + \sqrt[]{5})}{9 - 5} = k_{10} \frac{3 + \sqrt[]{5}}{2} . \end{matrix}

Minthogy

\begin{matrix} k_{10} = 10 \cdot \frac{r}{2} (\sqrt[]{5} - 1) = 5 r (\sqrt[]{5} - 1), \end{matrix}

\begin{matrix} s = 5 r \frac{(\sqrt[]{5} - 1) (3 + \sqrt[]{5})}{2} = 5 r (\sqrt[]{5} + 1) . \end{matrix}

A szabályos tízszögek hasonlók, tehát területük úgy aránylik egymáshoz, mint a megfelelő oldalak négyzetei. A sorban következő tízszögek területei tehát oly mértani haladványt alkotnak, melynek hányadosa

\begin{matrix} {(\frac{\sqrt[]{5} - 1}{2})}^{2} = \frac{5 - 2 \sqrt[]{5} + 1}{4} = \frac{3 - \sqrt[]{5}}{2} . \end{matrix}

A területek összege is összetartó; ha az első sokszög területe

t_{10}

, akkor a végtelen sok tízszög területének összege

\begin{matrix} σ = t_{10} \frac{1}{1 - \frac{3 - \sqrt[]{5}}{2}} = t_{10} \frac{2}{2 - 3 + \sqrt[]{5}} = t_{10} \frac{2}{\sqrt[]{5} - 1} = t_{10} \frac{\sqrt[]{5} + 1}{2} . \end{matrix}

Azonban

t_{10} = \frac{5 r^{2}}{2} \sqrt[]{\frac{5 - \sqrt[]{5}}{2}}

és így

\begin{matrix} σ = \frac{5 r^{2}}{2} \sqrt[]{\frac{5 - \sqrt[]{5}}{2}} \cdot \frac{\sqrt[]{5} + 1}{2} = \frac{5 r^{2}}{4} \sqrt[]{\frac{(5 - \sqrt[]{5}) {(5 + 1)}^{2}}{2}} = \frac{5 r^{2}}{4} \sqrt[]{(5 - \sqrt[]{5}) (3 + \sqrt[]{5})} = \\ = \frac{5 r^{2}}{4} \sqrt[]{10 + 2 \sqrt[]{5}} = \frac{5 r^{2}}{2} \sqrt[]{\frac{5 + \sqrt[]{5}}{2}} . \end{matrix}

Herczeg Gyula (Széchenyi István gyakorló r. VII. o. Pécs.)

¹Azt is mondhatjuk, hogy

A_{1} O A_{4}

egyenlőszárú háromszögben az

A_{t} O A_{4} ∢ = 3 \cdot 36^{0} = 108^{0}

, tehát az

A_{1} A_{4}

alapon fekvő szögek mindegyike

36^{\circ}

^{$^{*}$}Ha $r$ a szab. tízszög köré írt kör sugara $a_{ω} : r = (r - a_{ω}) : a$ . Aranymetszés.