Kezdőlap


Feladat:	1192. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barabás J. , Gergely J. , Kádár Gy. , Kardos Gy. , Kepes Á. , Komlós J. , Kukorelly Gy. , Nagy Elemér , Pálos Peregrin , Somogyi Éva , Szak Á. , Szmák L.
Füzet:	1936/március, 211 - 212. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1936/január: 1192. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $k$ körbe írt $A B C D$ húrnégyszög $A B$ , $B C$ , $C D$ , $D A$ oldalai, mint húrok fölött a $k_{1}$ , $k_{2}$ , $k_{3}$ , $k_{4}$ köröket szerkesztjük. Így keletkezik, az utóbbi körök metszéspontjai által az $F G H I$ négy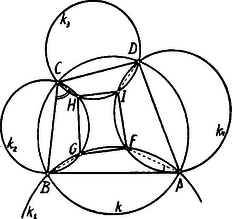szög.

Mármost

\begin{matrix} F G H ∢ = 360^{\circ} - B G F ∢ - B G H ∢ . \end{matrix}

(1)

Azonban

A B G F

k_{1}

körbe,

B G H C

k_{2}

körbe írt húrnégyszög és ezért

\begin{matrix} B G F ∢ = 180^{\circ} - B A F ∢ \end{matrix}

és

\begin{matrix} B G H ∢ = 180^{\circ} - B C H ∢ . \end{matrix}

Helyettesítve ezeket (1)-be, keletkezik

\begin{matrix} F G H ∢ = B A F ∢ + B C H ∢ . \end{matrix}

(2)

Hasonlóan:

\begin{matrix} F I H ∢ = D C H ∢ + D A F ∢ . \end{matrix}

(3)

Eszerint:

\begin{matrix} F G H ∢ + F I H ∢ = (B A F ∢ + D A F ∢) + (B C H ∢ + D C H ∢) = B A D ∢ + B C D ∢ = 180^{\circ} . \end{matrix}

Amint látjuk,

F G H I

négyszögben két szemben fekvő szög összege

180^{\circ}

, tehát

F G H I

húrnégyszög.

Pálos Peregrin (Bencés rg. VII. o. Pápa.)

Jegyzet. A következő feladat szempontjából újra kiemeljük, hogy a húrnégyszög két szemben fekvő oldala antiparallel helyzetű a másik két oldalra nézve.