Feladat:	1169. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Erdős Gábor ,  Gergely János ,  Lóránd E.
Füzet:	1936/január, 151. oldal		PDF  |  MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1935/november: 1169. matematika feladat

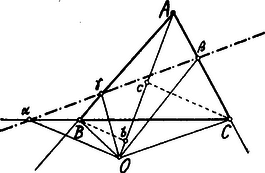
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Ki kell mutatnunk, hogy $\begin{array}{c}{\displaystyle \frac{\overline{\alpha B}}{\overline{\alpha C}}\cdot \frac{\overline{\beta C}}{\overline{\beta A}}\cdot \frac{\overline{\gamma A}}{\overline{\gamma B}}=1.}\end{array}$ (1) A $B$, $C$ pontoknak az $OA$ egyenesen való merőleges vetületei legyenek $b$, $c$. Így a $BC$ és $OA$ egyeneseket három párhuzamos egyenes metszi: $O\alpha$, $Bb$, $Cc$; ezek által létesített megfelelő szeletek aránya egyenlő, azaz $\begin{array}{c}{\displaystyle \frac{\overline{\alpha B}}{\overline{Ob}}=\frac{\overline{\alpha C}}{Oc}\text{vagy}\frac{\overline{\alpha B}}{\alpha C}=\frac{\overline{Ob}}{Oc}\mathrm{.}}\end{array}$ (2) Az $\overline{Ob}$ és $\overline{Oc}$ szeleteket az $\overline{OA}$ irányában vegyük pozitívnak; így $\begin{array}{c}{\displaystyle \overline{Ob}=OB\text{cos}AOB\sphericalangle \text{és}\overline{Oc}=\overline{OC}\text{cos}AOC\sphericalangle \mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle \frac{\overline{\alpha B}}{\overline{\alpha C}}=\frac{\overline{OB}}{\overline{OC}}\cdot \frac{\text{cos}AOB\sphericalangle }{\text{cos}AOC\sphericalangle }\mathrm{.}}\end{array}$ (3) Hasonlóan keletkezik (ciklikus permutációval) $\begin{array}{c}{\displaystyle \frac{\overline{\beta C}}{\overline{\beta A}}=\frac{\overline{OC}}{\overline{OA}}\cdot \frac{\text{cos}BOC\sphericalangle }{\text{cos}BOA\sphericalangle }}\end{array}$ (4) és $\begin{array}{c}{\displaystyle \frac{\overline{\gamma A}}{\overline{\gamma B}}=\frac{OA}{OB}\cdot \frac{\text{cos}COA\sphericalangle }{\text{cos}COB\sphericalangle }\mathrm{.}}\end{array}$ (5) A (3), (4), (5) egyenletek megfelelő tagjainak szorzásával az (1) egyenlethez jutunk. 1   Erdős Gábor (Toldy Ferenc r. VIII. o. Bp. II.) Gergely János (Berzsenyi Dániel rg. VIII. o. Bp. V.) 1$\text{cos}AOB=\text{cos}BOA$ s. í. t.