Feladat:	1156. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	B. Major P. ,  Boa P. ,  Bodó Z. ,  Erdős G. ,  Farkas I. ,  Frankl O. ,  Gergely J. ,  Gyulai L. ,  Harsányi J. ,  Herczeg Gy. ,  Ilkovits I. ,  Kardos Gy. ,  Kemény Gy. ,  Kepes Á. ,  Komlós J. ,  Lusteiner Gy. ,  Mandl B. ,  Müller S. ,  Nagy Elemér ,  Paulicsek J. ,  Pázmándi L. ,  Pick Gy. ,  Reiner I. ,  Rosenwald Gy. ,  Schreiber B. ,  Schwarz J. ,  Schwarz O. ,  Singer G. ,  Somogyi Antal ,  Somogyi Éva ,  Szele T. ,  Szmák Z.
Füzet:	1935/december, 113 - 114. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1935/október: 1156. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.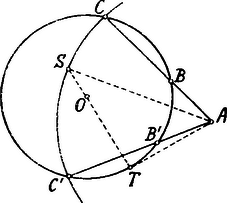   Minthogy $BC=AC-AB$, a feladat követelményét írhatjuk így is: $\begin{array}{c}{\displaystyle AC\left(AC-AB\right)=a^2\text{vagy}{\overline{AC}}^2=AC\cdot \overline{AB}+a^2\mathrm{.}}\end{array}$ A körön kívül fekvő $A$ pontból húzható szelőkre nézve azonban áll: $\begin{array}{c}{\displaystyle \overline{AC}\cdot \overline{AB}={\overline{AT}}^2\mathrm{,}}\end{array}$ ahol $T$ az $A$-ból, a körhöz húzott egyik érintő érintési pontja. Eszerint $\begin{array}{c}{\displaystyle {\overline{AC}}^2={\overline{AT}}^2+a^2\mathrm{,}}\end{array}$ azaz $AC$ oly derékszögű háromszög átfogója, melynek befogói $a$ és $\overline{AT}$. Ábránkban $a=ST$ úgy, hogy $ST\perp AT$. Eszerint $AS=AC$. $A$ pontból az $AS$ sugárral szerkesztett kör az $O$ kört a $C$ (ill. $C\text{'}$) pontban metszi. Helyzet szerint két megoldás van (az $OA$-ra nézve szimmetrikusan). Kössük össze $A$-t a kör $O$ középpontjával; az összekötő egyenes a kört a $D$ és $E$ pontban messe, úgy, hogy $AE>AD$. Hogy a feladatnak legyen megoldása, nyilván szükséges és elegendő, hogy $AC\le AE$ legyen. Ha $OA=d$ és a kör sugara $r$, akkor $AE=d+r$ és ${\overline{AT}}^2=d^2-r^2$. Az $AC\le AE$ feltétel írható: $\begin{array}{c}{\displaystyle \sqrt[]{a^2+d^2-r^2}\le d+r\mathrm{,}\text{vagy}{a}^2+d^2-r^2\le d^2+2dr+r^2\mathrm{,}}\end{array}$ és innen $\begin{array}{c}{\displaystyle a^2\le 2r\left(d+r\right)\text{ vagyis }{a}^2\le DE\cdot AE\mathrm{.}}\end{array}$ Nyilván: $BC\le DE$ és $AC\le AE$, tehát $\overline{BC}\cdot \overline{AC}=a^2\le \overline{DE}\cdot \overline{AE}$. Az $\overline{AC}\cdot \overline{BC}$ szorzatnak alsó határa csak zérus lehet, t. i. akkor, amidőn $BC=0$, azaz amidőn a szelőből érintő lesz.   Somogyi Antal (Gyakorló középiskola VI. o. Bp.)