Feladat: 1133. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bálint J. ,  Holzer Pál ,  Kardos Gy. ,  Komlós J. ,  Pick György ,  Schvarcz J. ,  Somogyi Éva ,  Szak Á. ,  Személyi K. 
Füzet: 1935/október, 53 - 55. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):Feladatok: 1935/május: 1133. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az X'X ill. Y'Y egyenes legyen a 2a ill. mellékszögének felezője, tehát az A csúcs egy derékszögű koordinátarendszer kezdőpontja. A háromszög megszerkesztésére elegendő a B pont helyzetét meghatározni. Ennek azon AZ egyenesen kell feküdnie, mely AX-hez α szög alatt hajlik.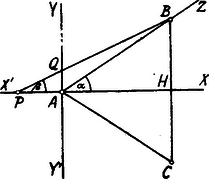

 
 

AH=x a B pont abscisszája, BH=y az ordinátája; tehát BC=2y. A feladat követelménye már most, hogy a B pont koordinátái között
2y-x=d
összefüggés álljon elő. Eszerint a B pont oly egyenesen fekszik, mely az X tengelyt y=0, x=-d pontban (P) metszi, míg az Y-tengelyt x=0, y=d2 pontban (Q). A P és Q pontok meghatározzák az e egyenest, mely AZ-t a B pontban metszi.
Taglalás. 1∘. Feltételezhetjük (ábránk szerint), hogy BC>AH, azaz d>0. Hogy a feladatnak legyen megoldása, szükséges és elegendő, hogy PQ az X-tengely fölött messe AZ-t, azaz ha APQ∢=β, akkor α>β legyen. A β szög ismeretes, mert oly derékszögű háromszög kisebbik szöge, amelyben az egyik befogó a másiknak kétszerese.
Ha α=β, akkor AZ||PQ; ekkor nincs megoldás.
Ha α<β, akkor AZ és PQ az X-tengely alatt metszik egymást, tehát a feladatnak nincs megoldása.
2∘. d=0 esetben mindazon egyenlő szárú háromszögekben, amelyekre nézve BC-AH=0 vagyis 2BH=AH, az A csúcsnál fekvő szög 2β tartozik lenni. Ha tehát α≠β, a feladat ellenmondást tartalmaz. Ha pedig α=β akkor a feladat határozatlan: végtelen sok megoldása van, az AZ egyenes minden pontja lehet a B csúcs.
3∘. d<0 esetben a P pont az X-tengelyen A-tól jobbra, a Q pont az Y-tengelyen A alatt fekszik. Ezen esetben APQ∢=β ugyanazon értékkel bír mint előbb (1∘ alatt); hogy PQ az AZ egyenest az X-tengely felett messe, szükséges és elegendő, hogy α<β legyen.
 

Holzer Pál (Faludi Ferenc rg. V. o. Szombathely)
 

II. Megoldás. Minthogy BH=AHtgα és BC=2BH=2AHtgα, következik:
BC-AH=AH(2tgα-1)=d,tehátAH=d2tgα-1.
Továbbá
BC=d+AH=2dtgα2tgα-1.

Ha d>0, kell, hogy 2tgα-1>0, azaz tgα>12 legyen. Található oly β hegyesszög, amelyre nézve tgβ=12, tehát
tgα>tgβvagyisα>βlegyen.

Ha d=0 és α≠β, akkor AH=0, BC=0, azaz nincs háromszög. α=β esetben a feladat határozatlan. (AH=00, bármely érték!)
d<0esetben kell, hogyα<βlegyen.β=26∘34'!

Pick György (Bolyai r. VII. o. Bp. V.)