Kezdőlap


Feladat:	1098. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	B. Major P. , Bauer Gy. , Beregi L. , Bodó Z. , Bródy Éva , Csanádi Gy. , Czégé I. , Fábián J. , Fenyő I. , Fenyvesi E. , Fischmann Éva , Földesi T. , Gergely J. , Győző F. , Halmágyi Z. , Hümpfner Olga , ifj. vitéz Verebély L. , Ilkovits I. , Kádár Gy. , Kálmán L. , Kedvessy K. , Kemény Gy. , Komlós J. , Oroszhegyi Szabó Lajos , Pick Gy. , Pulay M. , Róth Gy. , Rott M. , Schwarcz J. , Somogyi Éva , Spitzer R. , Steiner Z. , Szak Á. , Szeliczky D. , Személyi K. , Turda E. , Vajda A. , Valatin J. , Vass T.
Füzet:	1935/április, 230 - 231. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Vetítések, Derékszögű háromszögek geometriája, Terület, felszín, Téglalapok, Feladat
Hivatkozás(ok):	Feladatok: 1935/február: 1098. matematika feladat

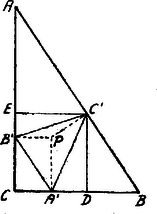
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $P$ pont mindig a $C D C' E$ téglalapon belül esik; ebből következik, hogy

\begin{matrix} C' E > P B' és C' D > P A' . \end{matrix}

(1)

Tekintsük az

A' B' C' ▵

három részét:

P A' B' ▵

P B' C' ▵

- és

P C' A' ▵

-et.

P B' A' ▵

nyilván fele a

P B' C A'

téglalapnak, azaz

\begin{matrix} T_{P B' A'} = \frac{1}{2} T_{P B' C A'} . \end{matrix}

(2)

P B' C' ▵

- és

B' C' E ▵

-eknek közös magasságuk

B' E

; azonban az első alapja

P B'

kisebb, mint a második

C' E

alapja és így

\begin{matrix} T_{P B' C'} < T_{B' C' E} vagy T_{P B' C'} < \frac{1}{2} T_{P B' E C'} . \end{matrix}

(3)

P C' A' ▵

- és

C' A' D ▵

-eknek közös magasságuk

A' D

; azonban az előbbi alapja

P A'

kisebb, mint a másodiknak

C D

alapja; ezért

\begin{matrix} T_{P C' A'} < T_{C' A' D} vagy T_{P C' A'} < \frac{1}{2} T_{P C' D A'} . \end{matrix}

(4)

A (2), (3), (4) megfelelő tagjait összegezve

\begin{matrix} T_{P B' A'} + T_{P B' C'} + T_{P C' A'} < \frac{1}{2} [T_{P B' C A'} + T_{P B' E C'} + T_{B C' D A'}] \end{matrix}

azaz

\begin{matrix} T_{A' B' C'} < \frac{1}{2} T_{C D C' E} . \end{matrix}

Oroszhegyi Szabó Lajos (Kegyesrendi g. VI. o. Bp.)