Kezdőlap


Feladat:	1094. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bak L. , Bauer Gy. , Csanádi Gy. , Czégé I. , Fenyő I. , Fischmann Éva , Fleischer Gy. , Gergely J. , Halmágyi Z. , Hümpfner Olga , Ilkovits Iván , Jász L. , Kádár Gy. , Kálmán L. , Kassai J. , Komlós J. , Pick Gy. , Pulay M. , Róth Gy. , Rott M. , Steiner Zoltán , Szele T. , Személyi K. , Valatin J. , Varga Z.
Füzet:	1935/április, 226 - 227. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1935/február: 1094. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A hiperbola egyenlete, főtengelyeire vonatkoztatva:

\begin{matrix} \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 ill. b^{2} x^{2} - a^{2} y^{2} = a^{2} b^{2} . \end{matrix}

(1)

A hiperbola

(x_{1}, y_{1})

pontjához tartozó érintő egyenlete:

\begin{matrix} \frac{x_{1} x}{a^{2}} - \frac{y_{1} y}{b^{2}} = 1, ill. b^{2} x_{1} x - a^{2} y_{1} y - a^{2} b^{2} = 0. \end{matrix}

(2)

Valamely

(x_{0}, y_{0})

pont távolsága a (2) egyenestől:

\begin{matrix} d = - \frac{b^{2} x_{1} x_{0} - a^{2} y_{1} y_{0} - a^{2} b^{2}}{\sqrt[]{b^{4} x_{1}^{2} + a^{4} y_{1}^{2}}} . \end{matrix}

(3)

A hiperbola gyújtópontjának koordinátái:

(\sqrt[]{a^{2} + b^{2}},0)

ill.

(- \sqrt[]{a^{2} + b^{2}},0)

. Eszerint:

\begin{matrix} d_{1} = - \frac{b^{2} x_{1} \sqrt[]{a^{2} + b^{2}} - a^{2} b^{2}}{\sqrt[]{b^{4} x_{1}^{2} + a^{4} y_{1}^{2}}}, d_{2} = - \frac{- b^{2} x_{1} \sqrt[]{a^{2} + b^{2}} - a^{2} b^{2}}{\sqrt[]{b^{4} x_{1}^{2} + a^{4} y_{1}^{2}}}, \\ d_{1} d_{2} = \frac{a^{4} b^{4} - b^{4} x_{1}^{2} (a^{2} + b^{2})}{b^{4} x_{1}^{2} + a^{4} y_{1}^{2}} = b^{4} \frac{a^{4} - x_{1}^{2} (a^{2} + b^{2})}{b^{4} x_{1}^{2} + a^{4} y_{1}^{2}} . & (4) \end{matrix}

Minthogy

(x_{1}, y_{1})

kielégítik az (1) egyenletet:

\begin{matrix} a^{2} y_{1}^{2} = b^{2} x_{1}^{2} - a^{2} b^{2} és a^{4} y_{1}^{2} = a^{2} b^{2} x_{1}^{2} - a^{4} b^{2} \\ b^{4} x_{1}^{2} + a^{4} y_{1}^{2} = b^{2} (a^{2} + b^{2}) x_{1}^{2} - a^{4} b^{2} = - b^{2} [a^{4} - x_{1}^{2} (a^{2} + b^{2})] . \end{matrix}

Helyettesítve ezt a (4) jobboldalán a nevezőbe, keletkezik

\begin{matrix} d_{1} d_{2} = \frac{b^{4} [a^{4} - x_{1}^{2} (a^{2} + b^{2})]}{- b^{2} [a^{4} - x_{1}^{2} (a^{2} + b^{2})]} = - b^{2} . \end{matrix}

d_{1} d_{2}

szorzat negatív, mert a gyújtópontok az érintő ellenkező oldalán feküsznek.

Steiner Zoltán (Árpád vezér rg. VIII. o. Bp. III.)

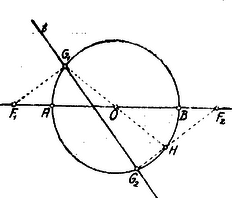
II. Megoldás. Jelöljék

F_{1}

F_{2}

a hiperbola gyújtópontjait,

O

a középpontját,

A

B

a csúcsait.

O A = O B = a

O F_{1} = O F_{2} = c = {(a^{2} + b^{2})}^{\frac{1}{2}}

. A

t

érintőre bocsátott merőlegesek talppontjai

G_{1}

G_{2}

. Ezek a hiperbola főkörén feküsznek, még pedig pl. úgy, hogy

F_{2} G_{2} > F_{1} G_{1}

F_{2} G_{2}

a főkört még egy

H

pontban metszi. Minthogy

F_{2} G_{2} G_{1} ∢ = 90^{\circ}

G_{1} H

a főkör átmérője, azaz

G_{1}

és

H

O

-ra nézve szimmetrikus pontok. Ebből következik, hogy

F_{2} H = F_{1} G_{1}

Ha a

t

érintő helyzetét változtatjuk, akkor

F_{2} G_{2}

F_{2}

körül forog, de minden helyzetben

\bar{F_{2} H} \cdot {\bar{F_{2} G}}_{2} = {\bar{F_{1} G}}_{1} \cdot {\bar{F_{2} G}}_{2} = constans =

F_{2}

pontnak a főkörre vonatkozó hatványával, tehát

\begin{matrix} | d_{1} d_{2} | = c^{2} - a^{2} = b^{2} . \end{matrix}

Ilkovits Iván (Kemény Zsigmond r. VII. o. Bp. VI.)