Kezdőlap


Feladat:	1086. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csanádi Gy. , Gergely János , Schuller I.
Füzet:	1935/március, 198 - 199. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Tengelyes tükrözés, Háromszögek nevezetes tételei, Szélsőérték-feladatok differenciálszámítás nélkül, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1935/január: 1086. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előző feladatban foglaltakra támaszkodva oldjuk meg ezt a feladatot.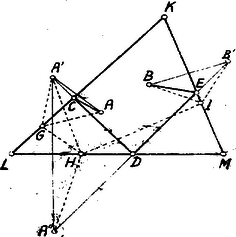

K L M ▵

-ben fekvő

A

és

B

pontokat összekötő törtvonal először a

K L

, azután az

L M

, végül az

M K

oldalon törik meg. Már most legyen az

A

szimmetrikusa a

K L

-re nézve

A'

, ennek szimmetrikusa

L M

-re nézve

A''

és

B

szimmetrikusa

M K

-ra nézve

B'

. Kössük össze

A''

-t

B'

-vel; az

A'' B'

egyenes az

L M

-et a

D

M K

-t az

E

pontban metszi. Továbbá az

A' D

egyenes a

K L

-t messe a

C

pontban. Így a keresett legrövidebb törtvonal:

A C D E B

.
A szimmetria miatt:

A C = A' C

;

\begin{matrix} A C + C D = A' C + C D = A' D = A'' D; \end{matrix}

továbbá

E B = E B'

. Eszerint

\begin{matrix} A C D E B = A C + C D + D E + E B = A'' D + D E + E B' = A'' B' . \end{matrix}

A C D E B

törtvonal hossza megegyezik az

A'' B'

távolságéval.
Legyen már most egy tetszőleges törtvonal

A G H I B

, úgy hogy

\begin{matrix} A G H I B = A G + G H + H I + I B . \end{matrix}

A szimmetria miatt:

A G = A' G

és

A' H = A'' H

; tehát

\begin{matrix} A G + G H = A' G + G H > A' H = A'' H . \end{matrix}

Másfelől

I B = I B'

; ennélfogva

\begin{matrix} A' G + G H + H I + I B > A'' H + H I + I B' > A'' B', \end{matrix}

azaz

\begin{matrix} A G H I B > A C D E B . \end{matrix}

Gergely János (Berzsenyi Dániel rg. VII. o. Bp. V.)

Jegyzet. Más törtvonalat kapunk, ha a törtvonal más sorrendben ér az oldalakhoz.
Ugyanezen feladatot a téglalapra nézve megoldottuk az I. évf. 93. oldalán, a 31. feladatban.
Ha

A

és

B

tetszőleges sokszögön belül fekszik, hasonló eljárás alapján oldjuk meg a feladatot.