Kezdőlap


Feladat:	1076. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Bauer Gy. , Csanádi Gy. , Czégé I. , Fenyő I. , Fischmann Éva , Fleischer Gy. , Gálik J. , Halmágyi Z. , Jász L. , Kádár Gy. , Kedvessy K. , Kepes Á. , Krausz J. , Kürthy Ö. , Magyar Károly , Pick Gy. , Pulay M. , Róth Gy. , Schreiber B. , Schuller I. , Schwarcz O. , Somogyi Éva , Szak Á. , Személyi K. , Valatin J.
Füzet:	1935/február, 167. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Gömb és részei, Feladat
Hivatkozás(ok):	Feladatok: 1934/december: 1076. matematika feladat

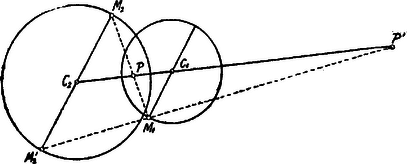
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Ha $C_{1} M_{1} ∥ C_{2} M_{2}$ , akkor ezek egy síkot határoznak meg; tehát $C_{1} C_{2}$ és $M_{1} M_{2}$ egyenesek is egy síkban vannak. Vegyük azon esetet, amidőn $C_{1} M_{1}$ és $C_{2} M_{2}$ ellentétes irányúak. Ha $M_{1} M_{2}$ és $C_{1} C_{2}$ metszéspontja $P$ , akkor $C_{1} M_{1} P ▵ \sim C_{2} M_{2} P ▵$ és így

\begin{matrix} P C_{2} : P C_{1} = C_{2} M_{2} : C_{1} M_{1} = r_{2} : r_{1}, \end{matrix}

(1)

ahol

r_{2}

ill.

r_{1}

C_{2}

ill.

C_{1}

gömb sugara.. Amint látjuk, a

P

pont a

C_{1} C_{2}

távolságot meghatározott arányban osztja két részre, függetlenül a

C_{1} M_{1}

ill.

C_{2} M_{2}

irányától, tehát szilárd pontja a

C_{1} C_{2}

egyenesnek.

Ha a

C_{1} M_{1}

és

C_{2} M_{2}

sugarakat ugyanolyan irányban húzzuk meg, az

M_{1} M_{2}

egyenes a

C_{1} C_{2}

, egyenest egy

P'

pontban metszi, amelyre nézve szintén áll:

\begin{matrix} P' C_{2} : P' C_{1} = C_{2} M'_{2} : C_{1} M_{1} = r_{2} : r_{1}, \end{matrix}

(2)

tehát

P'

is szilárd pont a

C_{1} C_{2}

, egyenesen.

2^{\circ}

. Az (1)-ből következik

\begin{matrix} \frac{P C_{2} + P C_{1}}{P C_{1}} = \frac{r_{1} + r_{2}}{r_{1}} . \end{matrix}

Minthogy

P C_{2} + P C_{1} = C_{1} C_{2} = d

\begin{matrix} P' C_{1} = \frac{d r_{1}}{r_{2} + r_{1}} és P' C_{2} = \frac{d_{2}}{r_{2} + r_{1}} \end{matrix}

A (2)-ből:

\begin{matrix} \frac{P' C_{2} - P' C_{1}}{P' C_{1}} = \frac{r_{2} - r_{1}}{r_{1}} . \end{matrix}

Minthogy most

P' C_{2} - P' C_{1} = d

\begin{matrix} P' C_{1} = \frac{d r_{1}}{r_{2} - r_{1}} és P' C_{2} = \frac{d r_{2}}{r_{2} - r_{1}} . \end{matrix}

Magyar Károly (Kegyesrendi rg. VII. o. Debrecen).