Kezdőlap


Feladat:	1071. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Csanádi Gy. , Czégé I. , Fenyő I. , Fenyvesi E. , Fischmann Éva , Gergely J. , Halmágyi Z. , Hümpfner Olga , Jász L. , Kádár Gy. , Kepes Á. , Krausz J. , Lusteiner Gy. , Pick Gy. , Pulay M. , Rott M. , Schuller I. , Somogyi Éva , Szele T. , Személyi K. , Valatin J.
Füzet:	1935/február, 160 - 161. oldal		PDF \| MathML
Témakör(ök):	Elemi függvények differenciálhányadosai, Parabola egyenlete, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1934/december: 1071. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . A két parabola $π_{1}$ és $π_{2}$ közös gyújtópontjuk legyen $O$ , csúcsuk $C_{1}$ ill. $C_{2}$ . Közös tengelyük a $C_{1} C_{2}$ egyenes; ezen fekszik $O$ . A két parabola közös tengelyükre nézve szimmetrikus pontokban metszi egymást ezek egyike legyen 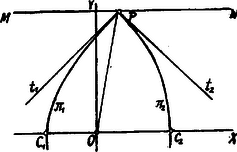$P$ .

Húzzuk meg a

P

ponton keresztül a tengelyükkel párhuzamos egyenest,

M N

-t. Ekkor a

π_{1}

parabola érintője a

P

pontban,

t_{1}

felezi az

\hat{M P O}

, a

π_{2}

parabola érintője,

t_{2}

felezi az

\hat{N P O}

szöget.

\hat{M P O}

és

\hat{N P O}

mellékszögek; már pedig mellékszögek felezői merőlegesek egymásra:

t_{1} ⊥ t_{2}

. Ez pedig ezt jelenti, hogy a két parabola merőlegesen metszi egymást!

2^{\circ}

. A két parabola közös tengelyét válasszuk a derékszögű koordinátarendszer

X

-tengelyének, közös gyújtópontjukat,

O

-t origónak. (Az

Y

tengely tehát ezen ponton megy keresztül.) A

π_{1}

parabola csúcsának koordinátái:

(- \frac{p_{1}}{2},0)

, a

π_{2}

csúcsáé:

(- \frac{p_{2}}{2},0)

\begin{matrix} π_{1} egyenlete : y^{2} = 2 p_{1} (x + \frac{p_{1}}{2}), & (1) \\ π_{2} egyenlete : y^{2} = - 2 p_{2} (x - \frac{p_{2}}{2}) . & (2) \end{matrix}

A két parabola közös pontjaira nézve

\begin{matrix} 2 p_{1} (x + \frac{p_{1}}{2}) = - 2 p_{2} (x - \frac{p}{2}) \\ azaz : 2 x (p_{1} + p_{2}) = p_{2}^{2} - p_{1}^{2} és x = \frac{p_{2} - p_{1}}{2} . & (3) \end{matrix}

Helyettesítve ezt akár (1)-be, akár (2)-be

\begin{matrix} y^{2} = p_{1} p_{2} . \end{matrix}

(4)

π_{1}

érintőjének,

t_{1}

-nek irányhatározója a közös

(x, y)

pontban:

\begin{matrix} y'_{1} = \frac{p_{1}}{y} . \end{matrix}

π_{2}

érintőjére nézve, ugyanott:

\begin{matrix} y'_{2} = - \frac{p_{2}}{y} . \end{matrix}

A két érintő merőleges egymásra, ha

y'_{1} y'_{2} = - 1

.
Azonban:

\begin{matrix} y'_{1} y'_{2} = - \frac{p_{1} p_{2}}{y^{2}}, \end{matrix}

(4) szerint

y^{2} = p_{1} p_{2}

, tehát valóban:

y'_{1} y'_{2} = - 1

Hümpfner Olga (Szent Orsolyarendi leányg. VIII. o. Sopron).