Kezdőlap


Feladat:	1070. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Anton J. , Bak L. , Balázs M. , Bálint J. , Csanádi Gy. , Czégé I. , Fenyő I. , Fenyvesi E. , Fischmann Éva , Fleischer Gy. , Freund K. , Gergely J. , Győző F. , Hümpfner Olga , Jacoby György , Jász L. , Kádár Gy. , Kálmán L. , Kedvessy K. , Kepes Á. , Kiss M. , Kovács László , Krausz J. , Lusteiner Gy. , Nagy Gy. , Pichler Gy. , Pick Gy. , Pulay M. , Róth Gy. , Rott M. , Schvarcz O. , Selig K. , Somogyi Éva , Sorok J. , Spitzer R. , Szele T. , Személyi K. , Valatin J. , Varga Z. , Vass T. , Villani Frigyes
Füzet:	1935/február, 159 - 160. oldal		PDF \| MathML
Témakör(ök):	Elemi függvények differenciálhányadosai, Egyenesek egyenlete, Kör egyenlete, Parabola egyenlete, Síkbeli szimmetrikus alakzatok, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1934/december: 1070. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A keresett kör középpontjának a parabola szimmetriatengelyén kell feküdnie, tehát a koordinátarendszer $X$ -tengelyén. Ha így a kör középpontjának koordinátát $(α,0)$ , a kör egyenlete

\begin{matrix} {(x - α)}^{2} + y^{2} = r^{2} . \end{matrix}

(1)

A parabola gyújtópontjának koordinátái:

(\frac{p}{2},0)

. Az

x = \frac{p}{2}

abcisszához tartozó parabola-pontok ordinátái

\pm p

.
Az (1) kör az

y^{2} = 2 p x

, parabolát érinti a

(\frac{p}{2}, p)

pontban, tehát itt közös érintőjük van. A kör

(x, y)

pontjában húzott érintőjének irányhatározóját megkapjuk, ha az (1) egyenletét

x

szerint differenciáljuk:

\begin{matrix} 2 (x - α) + 2 y y' = 0 és innen y' = - \frac{x - α}{y} . \end{matrix}

(2)

A parabola érintőjének irányhatározóját a parabola egyenletéből hasonlóan nyerjük:

\begin{matrix} 2 y y' = 2 p, azaz y' = \frac{p}{y} . \end{matrix}

(3)

(\frac{p}{2}, p)

ponthoz tartozó közös érintőre nézve

\begin{matrix} - \frac{\frac{p}{2} - α}{p} = \frac{p}{p}, tehát α = \frac{3 p}{2} . \end{matrix}

(4)

Az (1) kör keresztül megy a

(\frac{p}{2}, p)

ponton, tehát

\begin{matrix} {(\frac{p}{2} - \frac{3 p}{2})}^{2} + p^{2} = r^{2} vagyis r^{2} = 2 p^{2} . \end{matrix}

A keresett kör egyenlete szerint:

{(x - \frac{3 p}{2})}^{2} + y^{2} = 2 p^{2}

vagy:

\begin{matrix} x^{2} - 3 p x + y^{2} + \frac{p^{2}}{4} = 0. \end{matrix}

Jacoby György és Kovács László (Bencés g. VII. o. Esztergom).

II. Megoldás. Legyen

P

a parabola gyújtópontján átmenő és tengelyére merőleges húr felső végpontja

(y > 0)

. Ezen

P

pont ordinátája

P F = p

egyenlő a

P

pontnak a parabola vezérvonalától való távolsággal,

P M

-mel. A

P

pontban húzott érintő felezi az

F P M ∢

-et, tehát ezen érintő az

F P M N

négyzet átlója, ahol

N

a parabola vezérvonalának és tengelyének a metszéspontja. Ebből következik, hogy a

P

pontban húzott érintő a parabola tengelyéhez, a koordinátarendszerünk

X

-tengelyéhez

45^{\circ}

-ú szög alatt hajlik.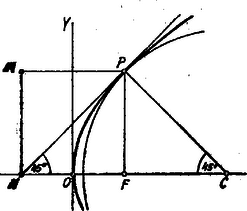

Húzzunk a

P

pontban a

P N

érintőre merőlegest; a keresett kör

C

középpontjának ezen egyenesen kell feküdnie, még pedig ott, ahol ezen egyenes az

X

-tengelyt metszi. Az előbbiekből következik, hogy

P C F ∢ = 45^{\circ}

, tehát

F C = p

és

C P = p \sqrt[]{2}

. A

C

pont abcisszája:

O C = O F + F C = \frac{p}{2} + p = \frac{3 p}{2}

; a kör sugara

C P = p \sqrt[]{2}

, tehát a kör egyenlete

\begin{matrix} {(x - \frac{3 p}{2})}^{2} + y^{2} = 2 p^{2} . \end{matrix}

Br. Villani Frigyes (Premontrei rg. VII. o. Gödöllő).