Kezdőlap


Feladat:	1052. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Csanádi Gy. , Czégé I. , Fábián J. , Fenyő I. , Fischmann Éva , Jász L. , Kádár Gy. , Kálmán L. , Krausz J. , Ozsdolay Gy. , Pick Gy. , Pulay M. , Rolich A. , Schvarcz O. , Szak Á. , Szeliczky D. , Személyi K. , Vass T.
Füzet:	1934/december, 103 - 104. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Derékszögű háromszögek geometriája, Szerkesztések a térben, Térgeometriai bizonyítások, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1934/október: 1052. matematika feladat

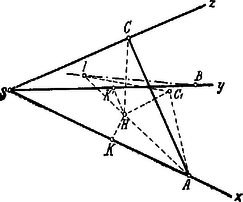
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . A $C$ pontból az $S x y$ síkra bocsátott merőleges talppontja legyen $H$ ; a $C$ pont távolsága az $S x y$ síktól $C H$ .
A $H$ pontból az $S x$ élre állított merőleges talppontja $K$ , az $S y$ élre állított merőlegesé $K'$ .

Ekkor

C K ⊥ S x

és

C K ⊥ S y

; ebből következik, hogy

S C K Δ ≅ S C K' Δ

. (Mindkettő derékszögű,

\hat{C S K} = \hat{C S K'} = 60^{\circ}

és az

S

C álfogójuk közös). Eszerint

S K = S K'

és

C K = C K'

és ezért

C H K Δ ≅ C H K' Δ

. (Két derékszögű háromszög, közös

C H

befogóval és

C K = C K'

). Ezen egybevágóság folytán

H K = H K'

, azaz a

H

pont az

S x

és

S y

élektől egyenlő távolságban van,

S H

felezi az

\hat{x S y} = 60^{\circ}

-ú szöget.^{$^{*}$}
Már most az

S C H Δ

-ből

\begin{matrix} {\bar{C H}}^{2} = {\bar{S C}}^{2} - {\bar{S H}}^{2} = c^{2} - {\bar{S H}}^{2} \end{matrix}

(1)

S H K Δ

-ből

\begin{matrix} S H = \frac{S K}{cos 30^{\circ}}; az S C K Δ -ből S K cos 60^{\circ} = c cos 60^{\circ} . \end{matrix}

\begin{matrix} S H = \frac{c \cdot cos 60^{\circ}}{cos 30^{\circ}} = \frac{c \cdot sin 30^{\circ}}{cos 30^{\circ}} = c \cdot tg 30^{\circ} = \frac{c \sqrt[]{3}}{3} . \end{matrix}

(2)

Helyettesítve

S H

értékét (1)-be

\begin{matrix} {\bar{C H}}^{2} = c^{2} - \frac{c^{2}}{3} = \frac{2 c^{2}}{3}, C H = c \sqrt[]{\frac{2}{3}} . \end{matrix}

2^{\circ}

. Ha a

B

S y

él oly pontja, amelyre nézve

A C B ∢ = 90^{\circ}

, akkor

C B

oly síkban fekszik, amelyet a

C

pontban

A C

-re merőlegesen fektettünk. Ezen síknak az

S x y

síkkal való metszésvonala legyen

B I

, ahol

I

A H

-val való metszéspontot jelzi. Minthogy

C H ⊥ [S x y]

, azért

C H ⊥ B I

; mivel

A C ⊥ [C B I]

, azért

A C ⊥ B I

. Eszerint

B I ⊥ [A C H]

, ebből pedig

B I ⊥ A H

. Másrészt

A C ⊥ C I

, azaz az

A C I

derékszögű háromszögben

\bar{A H} \cdot \bar{H I} = {\bar{C H}}^{2}

. Ezáltal az

I

pont helyzete az

A H

-n megvan határozva;

A I

-re merőlegest állítunk az

I

pontban, ez meghatározza az

S y

él

B

pontját.
A szerkesztést az

S x y

síkban következőképpen végezzük el:

A H

-ra a

H

pontban merőlegest állítva, felmérjük rá a

H C_{1} = H C

távolságot.

A C_{1}

-re a

C_{1}

-ben merőlegest állítunk; ezen merőleges

A H

meghosszabbítását az

I

pontban metszi.

^{$^{*}$}Röviden mondhattuk volna: a szimmetria miatt

H

pont egyenlő távolságban van az

S x

és

S y

élektől.