Kezdőlap


Feladat:	980. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bauer Gy. , Deutsch E. , Erőd J. , Jász L. , Paál S. , Semadam K. , Székely I. , Vankó Richárd , Verebély L. , Vozáry P. , Ökrös J.
Füzet:	1934/március, 195 - 196. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Függvények folytonossága, Függvényvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 1934/január: 980. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megadott függvénykapcsolatot

\begin{matrix} (y - 3) x^{2} - p x + y - q = 0 \end{matrix}

(1)

alakban írjuk fel és megvizsgáljuk, minő

y

értékekhez tartoznak valós

x

értékek? Erre a kérdésre felvilágosítást ad az (1) discriminánsa:

\begin{matrix} D \equiv p^{2} - 4 (y - 3) (y - q) = - 4 y^{2} + 4 (q + 3 y) + p^{2} - 12 q . \end{matrix}

(2)

Valós

x

értékek elégítik ki az (1)-et, ha

D \geq 0

. Minthogy

D

y

oly másodfokú függvénye, melyben

y^{2}

együtthatója

< 0

D \geq 0

, ha

y_{1} \leq y \leq y_{2}

ahol

y_{1}

és

y_{2}

(

y_{1} < y_{2}

) a

D = 0

egyenlet gyökei. A feladat követelménye, hogy

y_{1} = - 3

és

y_{2} = 4

legyen, azaz

\begin{matrix} q + 3 = - 3 + 4 és \frac{p^{2} - 12 q}{- 4} = - 3 \cdot 4 \end{matrix}

és innen

\begin{matrix} q = - 2, p = \pm 2 \sqrt[]{6} . \end{matrix}

Eszerint két függvény felel meg a követelménynek.

y = \frac{3 x^{2} + 2 \sqrt[]{6} x - 2}{x^{2} + 1}

. Ezen függvény mindenütt folytonos az

x = - \infty

x = + \infty

intervallumában; nevezője sehol sem tűnhetik el. Változását a köv. táblázat tünteti fel.

\begin{matrix} \begin{matrix} x & - \infty & - \frac{2 + \sqrt[]{2}}{\sqrt[]{3}} & - \frac{1}{\sqrt[]{6}} & 0 & \frac{2 - \sqrt[]{2}}{\sqrt[]{3}} & \sqrt[]{6} & + \infty \\ - 3 & 4 \\ y & 3 & ↘ & 0 & ↘ & ↗ & - 2 & ↗ & 0 & ↗ & ↘ & 3 \\ min & max \end{matrix} \end{matrix}

y = 0

helyeket a

3 x^{2} + 2 \sqrt[]{6} x - 2 = 0

egyenlet gyökei szolgáltatják.

y

érték minimum, ill. maximum azon

x

értékeknél, amelyek az (1) gyökei a

D = 0

esetekben (t. i.

y_{1} = - 3

ill.

y_{2} = 4

értékek mellett). T. i. ekkor az (1) gyökei egyenlők, még pedig

\begin{matrix} x_{1} = \frac{+ p}{2 (y_{1} - 3)} = \frac{+ 2 \sqrt[]{6}}{2 \cdot (- 6)} = - \frac{1}{\sqrt[]{6}}; \\ x_{2} = \frac{p}{2 (y_{2} - 3)} = \frac{2 \sqrt[]{6}}{2 \cdot (4 - 3)} = \sqrt[]{6} . \end{matrix}

y = 3

egyenes a görbe aszimptotája.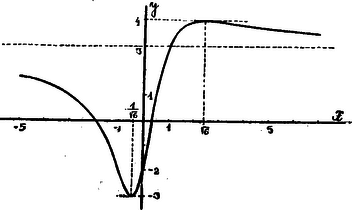

II.

y = \frac{3 x^{2} - 2 \sqrt[]{6} x - 2}{x^{2} + 1}

. Ezen függvényről is ugyanazt mondhatjuk, mint az előbbiről; változását jellemzi:

\begin{matrix} \begin{matrix} x & - \infty & - \sqrt[]{6} & - \frac{5}{2 \sqrt[]{6}} & \frac{- 2 + \sqrt[]{2}}{\sqrt[]{3}} & 0 & \frac{1}{\sqrt[]{6}} & \frac{2 + \sqrt[]{2}}{\sqrt[]{3}} & + \infty \\ 4 & - 3 \\ y & 3 & ↗ & ↘ & 3 & 0 & - 2 & 0 & 3 \\ max & min \end{matrix} \end{matrix}

\begin{matrix} y = 0, ha 3 x^{2} - 2 \sqrt[]{6} x - 2 = 0, azaz x = \frac{\sqrt[]{2} \pm 2}{\sqrt[]{3}} . \end{matrix}

A szélsőértékek helyeit az (1) egyenlet szolgáltatja a

D = 0

esetekben.
‐ A görbe az előbbivel szimmetrikus az origóra nézve.

Vankó Rihárd (Ág. ev. g. VIII. o. Bp.)