Kezdőlap


Feladat:	964. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csanádi Gy. , Czégé I. , Deutsch Ervin , Erőd J. , Faragó J. , Jász L. , Pohlencz A. , Porges A. , Pulay M. , Scheffer K. , Túri P. , Vankó R. , Varga Z. , Weiszfeld E.
Füzet:	1934/január, 141 - 142. oldal		PDF \| MathML
Témakör(ök):	Analógia, mint megoldási módszer, Súlyvonal, Négyszögek geometriája, Síkgeometriai számítások trigonometria nélkül négyszögekben, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1933/november: 964. matematika feladat

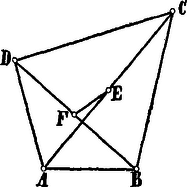
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Az $A C$ átló $E$ felezőpontját kössük össze a $B$ és $D$ csúcsokkal, továbbá a $B D$ átló $F$ felezőpontjával.

B E

A B C ▵

-nek

A C

oldalához,

D E

A C D ▵

A C

oldalához tartozó súlyvonal; érvényes tehát:

\begin{matrix} \bar{A B^{2}} + \bar{C B^{2}} = 2 \bar{B E^{2}} + \frac{\bar{A C^{2}}}{2}; \end{matrix}

Összegezve:

\begin{matrix} \bar{A B^{2}} + \bar{C B^{2}} + \bar{A D^{2}} + \bar{C D^{2}} = 2 \bar{B E^{2}} + 2 \bar{D E^{2}} + \bar{A C^{2}} . \end{matrix}

(1)

B D E ▵

-ben

E F

B D

-hez tartozó súlyvonal, tehát:

\begin{matrix} \bar{B E^{2}} + \bar{D E^{2}} = 2 \bar{E F^{2}} + \frac{\bar{B D^{2}}}{2} . \end{matrix}

Helyettesítsük ezt (1) jobboldalán:

\begin{matrix} \bar{A B^{2}} + \bar{C B^{2}} + \bar{A D^{2}} + \bar{C D^{2}} = 4 \bar{E F^{2}} + \bar{B D^{2}} + \bar{A C^{2}} ... \end{matrix}

Q. e. d.

2^{\circ}

. A tétel érvényes akkor is, ha az

A B C D

négyszög csúcsai nem feküsznek egy síkban, tehát egy tetraéder csúcsai. Az

A B C D

térnégyszög

A C

és

B D

átlói nem metszik egymást; de arra, hogy messék egymást, az

1^{\circ}

. alatti levezetésnél nincs szükség. Az

A C

és

B D

élek felezőpontjainak távolsága a tetraéder egyik ,,éltengelye''. Kimondhatjuk tehát, hogy az

A B C D

négyszög oldalait képező élek négyzetösszege a fennmaradó két él négyzetösszegénél az ezekhez tartozó éltengely négyzetének 4-szeresével nagyobb.

Deutsch Ervin (Faludi Ferenc rg. VIII. o. Szombathely)