Kezdőlap


Feladat:	938. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. , Boros A. , Buresch R. , Csanádi Gy. , Deutsch E. , Erőd J. , Erős Gy. , Feldmann J. , Gál E. , Gribács L. , Gyopár L. , Hirschler Z. , Holló Ágnes , Jachja L. , Janits I. , Jász L. , Kaiser F. , Kiss T. , Ottinger Gy. , Paál S. , Perneczky T. , Pick Gy. , Pikler F. , Pintér Gy. , Pohlencz A. , Pulay M. , Rézler Márta , Róth Sára , Rott M. , Sándor M. , Scheffer K. , Semadam K. , Spitz M. , Steiner Z. , Szabados Gy. , Taskó Gy. , Túri P. , Vankó Richárd , Verebély L. , Wagner W. , Weiszfeld E.
Füzet:	1933/november, 74 - 75. oldal		PDF \| MathML
Témakör(ök):	Síkidomok átdarabolása, Tengelyes tükrözés, Egyéb sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1933/szeptember: 938. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C$ hegyesszögű háromszög belsejében felvett $P$ pontnak a háromszög oldalaira vonatkozó tükörképei legyenek $P_{1}$ , $P_{2}$ , $P_{3};$ a szóban forgó hatszög csúcsai sorban 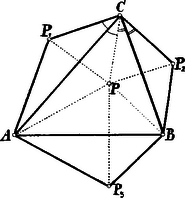$A$ , $P_{3}$ , $B$ , $P_{1}$ , $C$ , $P_{2} .$

P_{1}

P_{2}

P_{3}

csúcsoknál keletkező szögek a szimmetria miatt rendre a

B P C

C P A

A P B

szögekkel egyenlők; utóbbiak mindegyike

< 180^{\circ} .

A

B

C

csúcsoknál keletkező szögei a hatszögnek rendre

2 α

2 β

2 γ .

Minthogy

α

β

γ

a háromszög szögei hegyesszögek, a

2 α

2 β

2 γ

szögek mindegyike

< 180^{\circ} .

α

β

γ

egyike pl.

γ = 90^{\circ},

akkor

P_{1} C

P_{2}

egy egyenesbe esnek; a hatszög egyik szöge

180^{\circ} .

Ekkor tulajdonképpen konvex ötszöget kapunk.
Ha

γ > 90^{\circ},

akkor

P_{1} C P_{2} > 180^{\circ};

a hatszög konkáv.

Vankó Rikárd (Ágostai ev. gimn. VIII. o. Bp.).