Kezdőlap


Feladat:	925. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csanádi Gy. , Deutsch E. , Erőd J. , Makai E. , Manner L. , Weiszfeld Endre
Füzet:	1933/október, 47. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Háromszögek nevezetes tételei, Feladat
Hivatkozás(ok):	Feladatok: 1933/május: 925. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elegendő kimutatnunk, hogy a leghosszabb ív, t. i. a legnagyobb oldal végpontjain áthaladó, rövidebb a másik kettő összegénél. Legyen tehát $A B$ a háromszög legnagyobb oldala. Ha a háromszög hegyesszögű, akkor a $C$ csúcs ‐ amennyiben a tételben jelzett körök középpontjai az oldalakat felező merőlegeseknek a háromszögből kifelé irányuló részein feküsznek ‐ mindig az $A$ , $B$ csúcsokon áthaladó körön kívül fekszik; derékszögű és tompaszögű háromszög esetében akkor és csak akkor, ha $r > R$ . Utóbbi háromszögekre tehát a tétel (ill. ennek a köv. bizonyítása) csak $r > R$ esetben állhat meg.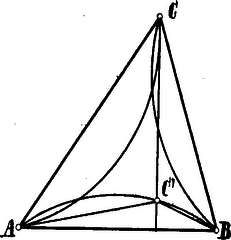
$C$ -ből a legnagyobb oldalra, $A B$ -re állított merőleges az $A B$ -t mindig $A$ és $B$ között, tehát az ${A B}_{}^{⌢}$ ívet is $A$ és $B$ között $C_{1}$ -ben metszi. Ekkor azonban, mivel $C_{1}$ közelebb van a $C$ -ből $A B$ -re állított merőleges talppontjához, mint $C$ , nyilván

\begin{matrix} {\bar{A C}}_{1} < \bar{A C} és {\bar{B C}}_{1} < \bar{B C} . \end{matrix}

Ugyanazon sugarú körökben, ezen húrokhoz tartozó ívekre érvényes:

\begin{matrix} {A C_{1}}_{}^{⌢} < {A C}_{}^{⌢} és {B C_{1}}_{}^{⌢} < {B C}_{}^{⌢} . \end{matrix}

Így

\begin{matrix} {A C_{1}}_{}^{⌢} + {B C_{1}}_{}^{⌢} = {A B}_{}^{⌢} < {A C}_{}^{⌢} + {B C}_{}^{⌢} . \end{matrix}

Weiszfeld Endre (Kemény Zsigmond r. VII. o. Bp.)

Kiegészítés: Ha tompaszögű háromszög esetében

r > R

, akkor a tompaszög

C

csúcsa az

A

B

pontokon áthaladó körön belül fekszik; a

C_{1}

pontra nézve ekkor

\begin{matrix} A C_{1} > A C és B C_{1} > B C, \end{matrix}

tehát

\begin{matrix} {A C_{1}}_{}^{⌢} > {A C}_{}^{⌢} és {B C_{1}}_{}^{⌢} > {B C}_{}^{⌢} . \end{matrix}

Most

\begin{matrix} {A C_{1}}_{}^{⌢} + {B C_{1}}_{}^{⌢} = {A B}_{}^{⌢} > {A C}_{}^{⌢} + {B C}_{}^{⌢} . \end{matrix}

r = R

, akkor

{A B}_{}^{⌢} = {A C}_{}^{⌢} + {B C}_{}^{⌢}

.
Derékszögű háromszög esetében csak

r \geq R

lehetséges;

r = R

mellett

\begin{matrix} {A B}_{}^{⌢} = {A C}_{}^{⌢} + {B C}_{}^{⌢} . \end{matrix}

Jegyzet. Abban az esetben, midőn

r > R

, képzelhetünk egy

r

sugarú gömböt, mely az

A

B

C

pontokon megy keresztül és egy háromélű testszögletet, melynek élei

O A

O B

O C

, ahol

O

a gömb középpontja. Az

r

sugarú kör, tehát a gömb főkörének ívei:

{A B}_{}^{⌢}

{A C}_{}^{⌢}

{B C}_{}^{⌢}

nem egyebek, mint az

O (A B C)

testszöglet oldalainak mértékei. Tehát a tételünk nem más, mint a három élű testszöglet oldalaira vonatkozó tétel: a három élű testszöglet két oldalának összege kisebb a harmadiknál.

Deutsch Ervin, Weiszfeld Endre.