Kezdőlap


Feladat:	921. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Buresch R. , Csanádi Gy. , Erőd J. , Geba I. , Jász Lajos , Kepes J. , Kiss T. , Lukács O. , Makai E. , Manner L. , Rott M. , Stolcz T. , Weiszfeld Endre
Füzet:	1933/október, 43 - 44. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1933/május: 921. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az adott $k$ kör $C$ középpontjából az adott egyenesre bocsátott egyenest válasszuk a koordinátarendszer abscissa-, az adott egyenest ordináta-tengelyéül. A $C$ pontnak a koordináta rendszer $O$ középpontjától való távolsága legyen $a$ , a kör sugara 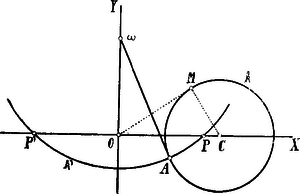$r$ .

Az ordináta-tengely változó

ω

pontjából

(0, q)

k

körhöz vont egyik érintő érintési pontja legyen

A

; ekkor az

ω

A

sugarú,

ω

középpontú

k'

kör egyenlete

\begin{matrix} x^{2} + {(y - q)}^{2} = {\bar{ω A}}^{2} . \end{matrix}

(1)

Azonban:

\begin{matrix} {\bar{ω A}}^{2} = {\bar{ω C}}^{2} - {\bar{A C}}^{2} = q^{2} + a^{2} - r^{2}, \end{matrix}

tehát helyettesítve ezt (1)-ben, a

k'

kör egyenlete:

\begin{matrix} x^{2} + y^{2} - 2 y q = a^{2} - r^{2} . \end{matrix}

Ezen kör az abscissa-tengelyt oly pontokban metszi, amelyekre nézve

y = 0

; tehát a metszéspontokra nézve

\begin{matrix} x^{2} = a^{2} - r^{2} és x = \pm \sqrt[]{a^{2} - r^{2}} . \end{matrix}

Ezen eredmény azt mutatja, hogy a

k'

kör az

X

-tengelyt mindenkor ugyanazon két pontban metszi; ezen pontok a szilárd

P

és

P'

pontok, mert

a

és

r

megadott állandók.
Ha

a = r

, azaz a

k

érinti az adott egyenest, akkor

x_{1} = x_{2} = 0

.
Ha

a < r

, azaz az adott egyenes metszi a

k

kört, akkor ilyen pontok (valós pontok) nincsenek.

Jász Lajos (Faludi Ferenc r. VI. o. Szombathely)

Jeyyzet.

a^{2} - r^{2}

O

pontnak a

k

körre vonatkozó hatványa; ha

O M

a kör érintője,

{\bar{O M}}^{2} = a^{2} - r^{2}

, tehát

O P = O P' = O M

II. Megoldás. A

k'

körökhöz a

C

pontból húzott érintők egyenlők (t. i. a

k

kör sugarával), tehát a

k'

köröknek közös hatványvonaluk van, mely a

C

ponton megy keresztül és merőleges a

k'

körök centrálisára, azaz az adott egyenesre. Ha e körök metszik ezen hatványvonalat, ennek két szilárd pontján mennek keresztül. Ez bekövetkezik akkor, ha az adott egyenes nem metszi a kört; ekkor ugyanis ‐ hogy az I. megoldás jeleit használjuk ‐

ω A ≧ ω O

; az egyenlőségi jel akkor áll elő, ha a

k

kör érinti az adott egyenest. Ha azonban az adott egyenes metszi a

k

kört, akkor

ω A < ω O

, tehát

k'

nem metszheti az

A

egyenest, mely

C

-ből az adott egyenesre merőlegesen húzható (valamint

k'

kör közös hatványvonalát).

Weiszfeld Endre (Kemény Zsigmond r. VII. o. Bp.)