Kezdőlap


Feladat:	912. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Emődi M. , Erőd J. , Geba I. , Kepes J. , Kiss T. , Makai E. , Manner László , Peuser G. , Singer I. (VIII. o.) , Sohr Anna , Spitz M. B. , Stolcz T. , Túri P. , Weiszfeld E.
Füzet:	1933/szeptember, 15 - 16. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Egyéb ponthalmazok a koordinátasíkon, Feladat
Hivatkozás(ok):	Feladatok: 1933/április: 912. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ellipszis egyenlete a főtengelyekre vonatkoztatva ( $a > b$ )

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1. \end{matrix}

(1)

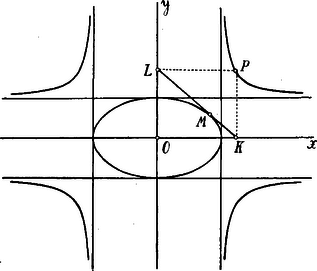
Az ellipszis

M

(

x_{0}

y_{0}

) pontjában húzott érintő egyenlete:

\begin{matrix} \frac{x_{0} x}{a^{2}} + \frac{y_{0} y}{b^{2}} = 1. \end{matrix}

(2)

Ezen érintő az

X

-tengelyt az

(y = 0, x = \frac{a^{2}}{x_{0}})

, az

Y

-tengelyt az

(x = 0, y = \frac{b^{2}}{y_{0}})

pontban metszi. Eszerint a

P

pont koordinátái

\begin{matrix} x = \frac{a^{2}}{x_{0}}, y = \frac{b^{2}}{y_{0}} . \end{matrix}

(3)

Meg kell állapítanunk, milyen összefüggés áll fenn

P

koordinátái között, ha (

x_{0}

y_{0}

) kielégítik az

\begin{matrix} \frac{x_{0}^{2}}{a^{2}} + \frac{y_{0}^{2}}{b^{2}} = 1 \end{matrix}

(4)

egyenletet? A (3) egyenletekből kifejezzük

x_{0}

y_{0}

értekét és (4)-be helyettesítjük:

\begin{matrix} x_{0} = \frac{a^{2}}{x}, y_{0} = \frac{b^{2}}{y}, \end{matrix}

tehát

\begin{matrix} \frac{a^{4}}{a^{2} x^{2}} + \frac{b^{4}}{b^{2} y^{2}} = 1, \end{matrix}

azaz

\begin{matrix} \frac{a^{2}}{x^{2}} + \frac{b^{2}}{y^{2}} = 1. \end{matrix}

(5)

Ezen egyenlet

y

ill.

x

szerint megoldva

\begin{matrix} y = \pm \frac{b x}{\sqrt[]{x^{2} - a^{2}}} és x = \pm \frac{a y}{\sqrt[]{y^{2} - b^{2}}} . \end{matrix}

Innen azt olvashatjuk ki, hogy a

P

pont a sík oly részeiben helyezkedik el, amelyre nézve:

| x | \geq a

és

| y | \geq b

. Az

x = \pm a

és

y = \pm b

egyenesek (az ellipszis csúcspontjaihoz tartozó érintők) az (5) görbe aszimptotái. A görbének 4 ága van; kettő-kettő szimmetrikus az

X

-tengelyre, ill. az

Y

-tengelyre, ill. az origóra nézve.

Manner László (Kölcsey Ferenc rg. VIII. o. Bp. VI.)