Kezdőlap


Feladat:	888. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. , Bihari I. , Bodori I. , Csató I. , Deutsch E. , Döme J. , Emődi M. , Erőd J. , Geba I. , Hegedűs Tibor , Kaiser F. , Kepes J. , Kiss T. , Lehr M. , Makai E. , Manner L. , Nagy D. , Pikler F. , Pulay M. , Réffy K. , Repper J. , Róth Sz. , Spitz M. , Szabó I. , Tarnóczy T. , Wagner W.
Füzet:	1933/április, 223 - 224. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Trigonometrikus egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 1933/február: 888. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Az $y$ függvény differenciálhányadosa

\begin{matrix} y' = 3 sin^{2} x cos x - 3 cos^{2} x sin x = 3 sin x cos x (sin x - cos x) . \end{matrix}

y' = 0

, ha a)

sin x = 0

, b)

cos x = 0

, c)

sin x - cos x = 0

vagyis

tg x = 1

\begin{matrix} a) sin x = 0, \\ ha & x = 0, π, 2 π . \\ b) cos x = 0, \\ ha & x = \frac{π}{2}, \frac{3 π}{2} . \\ c) tg x = 1, \\ ha & x = \frac{π}{4}, \frac{5 π}{4} . \end{matrix}

Megvizsgálva ezen helyeken

y'

előjelének változását és kiszámítva a megfelelő

y

értékeket, a köv. táblázatba foglalhatjuk:

\begin{matrix} x| & 0 & \frac{π}{4} & \frac{π}{2} & π & \frac{5 π}{4} & \frac{3 π}{2} & 2 π \\ y'| & 0 & - & 0 & + & 0 & - & 0 & + & 0 & - & 0 & + & 0 \\ y| & 1 & ↘ & \frac{\sqrt[]{2}}{2} & ↗ & 1 & ↘ & - 1 & ↗ & - \frac{\sqrt[]{2}}{2} & ↘ & - 1 & ↗ & + 1 \end{matrix}

y = 0

, ha

sin^{3} x = - cos^{3} x

vagyis

{tg}^{3} x = - 1

, tehát

tg x = - 1

és

\begin{matrix} x = \frac{3 π}{4}, \frac{7 π}{4} . \end{matrix}

2^{\circ}

. A

\begin{matrix} sin^{3} x + cos^{3} x = sin^{3} α + cos^{3} α \end{matrix}

(1)

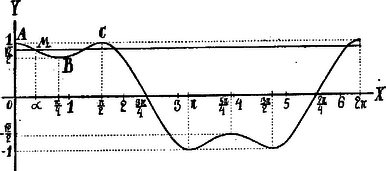
egyenlet megoldásai azon pontok abscissái, melyeknek ordinátái ugyanakkorák, mint az

α

abscissához tartozó

M

pont ordinátája. Ezeket megkapjuk, ha a függvény-görbét az

X

-tengellyel párhuzamos

\begin{matrix} y = sin^{3} α + cos^{3} α \end{matrix}

(2)

egyenessel szeljük.

α = 0

esetben az

y = 1

egyenes érinti a görbét az

x = 0

\frac{π}{2}

2 π

pontokban.

0 < α < \frac{π}{4}

értékek mellett az

M

pont az

A B

íven van; a (2) egyenes négy pontban metszi a görbét; kettő közülük

α

és

\frac{π}{2} - α

α = \frac{π}{4}

esetben az egyenes egyenlete:

y = \frac{\sqrt[]{2}}{2}

; ezen egyenes a

B

pontban

(x = \frac{π}{4})

érinti és még két pontban metszi a görbét.

Hegedüs Tibor (Szent István rg. VIII. o. Bp.)