Feladat:	865. matematika feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Asztalos E. ,  Baneth L. ,  Bihari I. ,  Csikós Nagy B. ,  Erőd J. ,  Felter K. ,  Geba I. ,  Kálmán E. ,  Kurz F. ,  Makai E. ,  Manner L. ,  Mérei L. ,  Nagy D. ,  Ottinger György ,  Pulay M. ,  Rácz Anna ,  Róth Sz. ,  Sohr Anna ,  Tóth Gy. ,  Weiszfeld E.
Füzet:	1933/február, 163 - 164. oldal		PDF  |  MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Trigonometrikus egyenletek, Paraméteres egyenletek, Gyökök és együtthatók közötti összefüggések, Trigonometriai azonosságok, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1932/december: 865. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.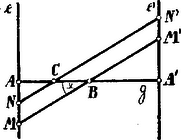   A feladat követelménye az $\begin{array}{c}{\displaystyle MM\text{'}+MN=l}\end{array}$ (1) egyenlet megoldása. Minthogy $B$ az $MM\text{'}$ és $N$ az $AM$ felezőpontja, $\begin{array}{c}{\displaystyle MM\text{'}=2MB=\frac{2AB}{\text{cos}x}=\frac{4a}{\text{cos}x};MN=AN=AC\text{tg}x=a\text{tg}x\mathrm{.}}\end{array}$ Eszerint (1)-ből: $\begin{array}{c}{\displaystyle \frac{4a}{\text{cos}x}+a\text{tg}x=l\text{vagy}l\text{cos}x-a\text{sin}x=4a\mathrm{.}}\end{array}$ (2) Ezen egyenlet megoldására célszerű $\text{sin}x$ és $\text{cos}x$-et $\text{tg}\frac{x}{2}$ segítségével kifejezni. Ezáltal $\begin{array}{c}{\displaystyle \frac{l\left(1-{\text{tg}}^2\frac{x}{2}\right)}{1+{\text{tg}}^2\frac{x}{2}}-\frac{2a\text{tg}\frac{x}{2}}{1+{\text{tg}}^2\frac{x}{2}}=4a}\end{array}$ ill. $\begin{array}{c}{\displaystyle \left(l+4a\right){\text{tg}}^2\frac{x}{2}+2a\text{tg}\frac{x}{2}+4a-l=0.}\end{array}$ (3) $x$ minden értékéhez tartozik egy második paralelogramma is, amely az elsővel szimmetrikus az $AA\text{'}$-re nézve; feltehetjük tehát, az általánosság megszorítása nélkül, hogy $x$ csak $0$ és $\frac{\pi }{2}$ között változik és így $\text{tg}\frac{x}{2}$ értéke $0$ és $\text{tg}\frac{\pi }{4}=1$ között kell, hogy legyen. A (3) egyenlet gyökei valósak, ha $\begin{array}{c}{\displaystyle 4a^2-4\left(l+4a\right)\left(4a-l\right)\geqq 0\text{azaz}l\geqq a\sqrt[]{15}\mathrm{.}}\end{array}$ A gyökök összege: $-\frac{2a}{l+4a}<0$; tehát vagy mind a két gyök negatív, vagy csak az egyik. Csak az utóbbi eset felelhet meg; ez pedig akkor áll elő, ha a gyökök szorzata: $\frac{4a-l}{l+4a}<0$, azaz, ha $l>4a$. Ha tehát $l>4a$, akkor a feladatnak van egy valós megoldása. $l=4a$ mellett, az egyenlet egyik gyöke: $\text{tg}\frac{x}{2}=0$ vagyis $x=0$. A paralelogramma az $AA\text{'}=4a$ vonaldarabbá válik.   Ottinger György (Érseki rg. VI. o. Bp. II.) Jegyzet. Az $a\sqrt[]{15}\leqq l<4a$ esetben a (3) egyenlet mindkét gyöke negatív. Ezeket pozitív jellel véve, oly $x$ szögeket kapunk, amelyek az $MM\text{'}-MN=l$ követelménynek megfelelő két paralelogrammát határoznak meg. (2)-ből $\begin{array}{c}{\displaystyle \frac{l}{a}\text{cos}x\text{sin}x=4.}\end{array}$ helyettesítéssel a $\begin{array}{c}{\displaystyle \frac{l}{a}=\text{cotg}\phi \text{helyettesítéssel}a\text{cos}\left(x+\phi \right)=4\text{sin}\phi }\end{array}$ egyenletet nyerjük, mely logarithmikus számításra alkalmas.