Feladat:	864. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. ,  Bihari I. ,  Buresch R. ,  Csikós Nagy B. ,  Emődi M. ,  Gribács L. ,  Kálmán E. ,  Kepes J. ,  Kiss T. ,  Makai E. ,  Manner L. ,  Mérei L. ,  Mihály J. ,  Nagy D. ,  Pikler F. ,  Réffy K. ,  Sohr Anna ,  Stekler E. ,  Stolcz T. ,  Szabó I. ,  Taskó György ,  Wagner W. ,  Weiszfeld E. ,  Wirth I.
Füzet:	1933/február, 162 - 163. oldal		PDF  |  MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Függvényvizsgálat differenciálszámítással, Tengely körüli forgatás, Parabola egyenlete, Egyenes körkúpok, Feladat
Hivatkozás(ok):	Feladatok: 1932/december: 864. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.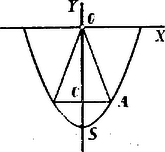   A kúp alapjának sugara $CA=x$ és $0\leqq x\leqq 2$; magassága $|y|$. Így az alkotó: $\begin{array}{c}{\displaystyle OA=\sqrt[]{x^2+|y{|}^2}=\sqrt[]{x^2-7x^2+16}\mathrm{.}}\end{array}$ A kúp palástja: $\begin{array}{c}{\displaystyle P=\overline{OA}\cdot \pi \cdot x=\pi \sqrt[]{x^6-7x^4+16x^2}\mathrm{.}}\end{array}$ A palást értékváltozásának vizsgálatára elegendő az $\begin{array}{c}{\displaystyle F\left(x\right)=x^6-7x^4+16x^2}\end{array}$ függvény változását vizsgálni, ha $0\leqq x\leqq 2$. Ha $x=0$, $F\left(0\right)=0$, a kúp palástja egyenes vonaldarabbá zsugorodik össze $\left(OS\right)$. Ha $x=2$, $F\left(2\right)=16$ és $P=4\pi$. A kúp palástja körré válik, melynek sugara $2$ egység. Az $F\left(x\right)$ függvény differenciálhányadosa: $\begin{array}{c}{\displaystyle F\left(x\right)=6x^5-28x^3+32x=2x\left(3x^4-14x^2+16\right)=6x\left(x^2-2\right)\left(x^2-\frac{8}{3}\right)\mathrm{.}}\end{array}$ mert $F\text{'}\left(x\right)=0$, ha $x^2=2$ vagy $x^2=\frac{8}{3}$. Ezzel kapcsolatban az $F\left(x\right)$ változását a köv. táblázattal jellemezhetjük: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cccccccc|}\hline \hfill {\displaystyle x}\hfill & \hfill {\displaystyle 0}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \sqrt[]{2}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \sqrt[]{\frac{8}{3}}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle 2}\hfill \\ \hfill {\displaystyle F\text{'}\left(x\right)}\hfill & \hfill {\displaystyle 0}\hfill & \hfill {\displaystyle +}\hfill & \hfill {\displaystyle 0}\hfill & \hfill {\displaystyle -}\hfill & \hfill {\displaystyle 0}\hfill & \hfill {\displaystyle +}\hfill & \hfill {\displaystyle +}\hfill \\ \hfill {\displaystyle F\left(x\right)}\hfill & \hfill {\displaystyle 0}\hfill & \hfill {\displaystyle \nearrow }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \searrow }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \nearrow }\hfill & \hfill {\displaystyle 16}\hfill \\ \hline\end{array}}}\end{array}$ Eszerint a kúp palástjának is van egy maximuma, ha 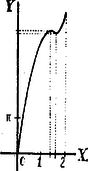$x=\sqrt[]{2}$, még pedig $\begin{array}{c}{\displaystyle P_{\underset{}{\overset{}{\text{max}}}}=\pi \sqrt[]{12}=2\pi \sqrt[]{3}\mathrm{,}}\end{array}$ továbbá egy minimuma, ha $x=\sqrt[]{\frac{8}{3}}$, még pedig $\begin{array}{c}{\displaystyle P_{\underset{}{\overset{}{\text{min}}}}=\pi \sqrt[]{\frac{320}{27}}=\frac{8\pi }{3}\sqrt[]{\frac{5}{3}}\mathrm{.}}\end{array}$   Taskó György (Szent László rg. VII. o. Bp. X.)   Jegyzet. A $2\pi \sqrt[]{3}$ és $\frac{8\pi }{3}\sqrt[]{\frac{5}{3}}$ értékek a kúppalást relatív szélső értékei. Az $x=2$ helyen abszolút maximuma van: $P=4\pi$; az $x=0$ helyen abszolút minimuma van: $P=0$.