Kezdőlap


Feladat:	831. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bihari I. , Döring A. , Emődi M. , Farkas V. , Geba I. , Hegedüs T. , Kaiser F. , Kálmán E. , Lehel P. , Lehr M , Makai Endre , Manner L. , Réffy K. , Róth Sára , Sohr Anna , Szabó Pap László , Weiszfeld E. , Zoldán E.
Füzet:	1932/november, 69 - 70. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Körök, Feladat
Hivatkozás(ok):	Feladatok: 1932/szeptember: 831. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A körnek $X' O X$ átmérőjén az $A$ és $B$ golyókat a $O$ középpont elválasztja egymástól. Ha pl. az $A$ golyót ellökve, ez a kör kerületének $C$ pontjába ütközik, akkor $O C$ a beesési merőleges és ennek másik oldalán pattan vissza a golyó úgy, hogy a beesési szög = a visszaverődési szöggel. Hogy tehát az $A$ golyó a $B$ -t találja, kell, hogy $O C$ az $A B C ▵$ -nek $A C B ∢$ -ét felezze, vagyis

\begin{matrix} A C : B C = A O : O B . \end{matrix}

Eszerint a

C

pontnak az

A

és

B

pontoktól való távolságainak viszonya meghatározott érték

(\frac{A O}{O B})

. Az ilyen tulajdonsággal bíró pontok mértani helye (az Apollonius-féle) kör. Az

X' X

egyenesen meghatározzuk azon

P

pontot, az

A B

-n kívül, amelyre nézve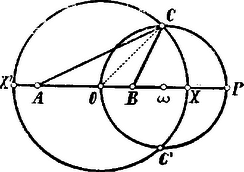

\begin{matrix} A P : B P = A O : O B \end{matrix}

¹.

O P

átmérő fölött szerkesztett kör a szóbanforgó tulajdonsággal rendelkező pontok mértani helye. Ezen körnek és az adott körnek közös pontjához kell az

A

golyót lökni, hogy visszaverődés után a

B

-t találja.
b) A feladatnak még egy másik megoldása az is, ha pl. az

A

golyót az

X' X

átmérőnek azon végpontja felé lökjük, amely hozzá közelebb esik. Ezen megoldás akkor is szóbajöhet, amidőn az

A

és

B

golyókat az

O

középpont nem választja el egymástól.

Makai Endre (Kegyesrendi g. VIII. o. Bp.)

¹A,BésO,Pharmonikuspontpárok