Kezdőlap


Feladat:	827. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. , Bihari I. , Böhm Anna , Csikós Nagy B. , Deutsch E. , Egyed L. , Emődi M. , Erőd J. , Farkas V. , Geba I. , Gerber E. , Gribács L. , Gyarmati B. , Hegedűs T. , Kaiser F. , Kálmán E. , Kaufmann I. , Kepes J. , Kérey H. , Kovács P. , Kováts I. , Lehel P. , Lehr M. , Lukács O. , Makai E. , Manner L. , Mérey L. , Nemes Ö. , Papp L. , Pataki E. , Pikler F. , Pintér Gy. , Pulay M. , Róth Sz. , Singer I. , Sohr Anna , Spitz M. , Stekler E. , Stolcz T. , Szabó I. , Tarnóczy T. , Vona Gy. , Wagner W. , Weiszfeld E.
Füzet:	1932/november, 65 - 66. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Téglatest, Terület, felszín, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1932/szeptember: 827. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A négyzetes oszlop $x$ alapélét válasszuk független változónak; a magassága legyen $m$ . Minthogy

\begin{matrix} F = 2 x^{2} + 4 x m, m = \frac{F - 2 x^{2}}{4 x} \end{matrix}

és az oszlop térfogata

\begin{matrix} y = x^{2} m = \frac{x^{2} (F - 2 x^{2})}{4 x} = \frac{x (F - 2 x^{2})}{4} . \end{matrix}

y

függvény változását vizsgálnunk kell az

x = 0

és

x = \sqrt[]{\frac{F}{2}}

értékek intervallumában. Ugyanis

F

kifejezéséből látjuk, hogy

\begin{matrix} 2 x^{2} \leq F, tehát 0 < x \leq \sqrt[]{\frac{F}{2}} . \end{matrix}

x = 0

, akkor

y = 0

és ha

x = \sqrt[]{\frac{F}{2}}

, szintén

y = 0

áll elő.

y

differenciálhányadosa,

\begin{matrix} y' = \frac{F - 6 x^{2}}{4} = 0, ha 6 x^{2} = F vagyis x = \sqrt[]{\frac{F}{6}}^{1} \end{matrix}

¹ Mivel pedig

y' > 0

, ha

x < \sqrt[]{\frac{F}{6}}

és

y' < 0

, ha

x > \sqrt[]{\frac{F}{6}}

, azért az

x = \sqrt[]{\frac{F}{6}}

helyen az

y

függvénynek maximuma van. A

6 x^{2} = F

egyenlet azt mutatja, hogy az egyenlő felületű négyzetes oszlopok között a kockának van legnagyobb térfogata és

\begin{matrix} y_{{max}_{}^{}} = \frac{\sqrt[]{\frac{F}{6}} (F - 2 \frac{F}{6})}{4} = {(\sqrt[]{\frac{F}{6}})}^{3} . \end{matrix}

A térfogat változását a köv. táblázat jellemzi: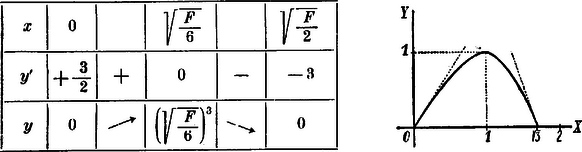

¹A jelzett intervallumban

x

csak poz. lehet.