Kezdőlap


Feladat:	812. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Bihari I. , Blazsek I. , Csikós Nagy B. , Deutsch E. , Döring A. , Egyed L. , Emődi M. , Geba I. , Gerber Zsuzsa , Giesser György , Gyarmati B. , Kalán J. , Kálmán E. , Kepes J. , Manner L. , Mérei L. , Papp L. , Pulay M. , Réffy K. , Singer G. , Singer I. , Skurek Z. , Stekler E. , Szabó István , Tarnóczy T. , Tóth L.
Füzet:	1932/október, 38 - 39. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Trapézok, Érintőnégyszögek, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1932/május: 812. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $O$ középpontú, $r$ sugarú kör köré írt $A B C D$ trapéz területét tekintsük az $A B = 2 x$ ill. $B E = x$ függvényének. Ha a $B C$ oldal a kört $F$ pontban érinti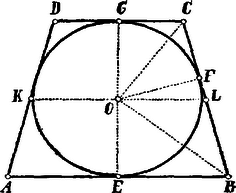, $B F = B E$ és $C F = C G$ .

B O C ▵

O

-nál derékszögű (mert

O C

és

O B

G O F ∢

és

F O E ∢

mellékszögeket felezik) és

O F ⊥ B C

; ezért

\begin{matrix} \bar{B F} \cdot \bar{C F} = {\bar{O F}}^{2} vagyis x \cdot C F = r^{2}, \end{matrix}

tehát

C F = \frac{r^{2}}{x}

. Így a trapéz területe

\begin{matrix} y = \frac{A B + C D}{2} \cdot E G = (x + \frac{r^{2}}{x}) 2 r \end{matrix}

és

\begin{matrix} y' = \frac{d y}{d x} = (1 - \frac{r^{2}}{x^{2}}) 2 r . \end{matrix}

x

értéke változik

0

-tól

+ \infty

-ig. A differenciálhányados

x = r

-nél eltűnik, ill. ha

x < r

, akkor

y' < 0

, ha

x > r

, akkor

y' > 0

; tehát

x = r

helyen az

y

függvénynek minimuma van. Ha

x

változik

0

és

r

között,

y

csökken

+ \infty

-től a minimumig; ha

x

változik

r

-től

+ \infty

-ig,

y

növekedik a minimumtól

+ \infty

-ig.
Ha

x = r

, a trapéz négyzetté válik és

y_{{min}_{}^{}} = 4 r^{2}

Giesser György (Klauzál Gábor rg. VII. o. Szeged)

II. Megoldás. A trapéz területe

\begin{matrix} t = \frac{A B + C D}{2} \cdot E F = K L \cdot 2 r . \end{matrix}

A trapéz középvonala,

K L

, a kör középpontján megy keresztül és

K L ≧ 2 r

. Eszerint a trapéz területe

\begin{matrix} t ≧ 4 r^{2}, \end{matrix}

tehát legkisebb akkor, amidőn

K L = 2 r

és

t_{{min}_{}^{}} = 4 r^{2}

Szabó István (Br. Eötvös József r. VII. o. Bp. VI.)