Kezdőlap


Feladat:	802. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alpár László , Blazsek I. , Emődi M. , Réffy K. , Weiszfeld E.
Füzet:	1932/szeptember, 16 - 18. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Determinánsok - lineáris egyenletrendszerek, Egyenes, Ellipszis, mint mértani hely, Hiperbola, mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1932/április: 802. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . A $P Q$ egyenes egyenlete, ha $O P = p$ , $O Q = q$ ,

\begin{matrix} \frac{x}{p} + \frac{y}{q} - 1 = 0, tehát m = - \frac{q}{p} . \end{matrix}

(1)

C P

ill.

D Q

egyenes egyenlete:

\begin{matrix} \frac{x - 2}{p - 2} & = \frac{y - 3}{- 3}, ill. & (2) \\ \frac{x - 3}{- 3} & = \frac{y - 4}{q - 4} . & (3) \end{matrix}

C P

és

D Q

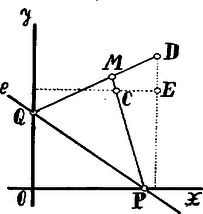egyenesek

M

metszéspontjának koordinátáit a (2) és (3) egyenletekből, mint

p

és

q

függvényeit számíthatjuk ki; hogy azonban az

M

pont

x

y

koordinátái között csak az

m

paramétertől függő egyenletet kapjunk, az (1), (2), (3) egyenletekből kiküszöböljük

p

-t és

q

-t. Így az

\begin{matrix} (y - 3) (4 x - 3 y) + m (x - 3) (2 y - 3 x) = 0 \end{matrix}

(4)

egyenlethez jutunk. Eszerint az

M

pont mértani helye egy kúpszelet, mely keresztülmegy a

\begin{matrix} C (2,3), D (3,4), E (3,3) és az O (0,0) \end{matrix}

pontokon. (A koordináta tengelyekkel való másik közös pontja könnyen meghatározható. Így már a kúpszelet

6

pontja lesz ismeretes).

2^{\circ}

. Hogy a (4) kúpszelet nemét meghatározhassuk, hozzuk azt

\begin{matrix} A x^{2} + 2 B x y + C y^{2} + 2 D x + 2 E y + F = 0 \end{matrix}

alakra és vizsgáljuk elsősorban

\begin{matrix} δ = A C - B^{2} = - (m - 1) (m - 4) \end{matrix}

azután

\begin{matrix} Δ = | \begin{matrix} A & B & D \\ B & C & E \\ D & E & F \end{matrix} | = - \frac{9}{4} m (m - 1) \end{matrix}

előjelét.

δ < 0

, ha

m < 1

vagy

m > 4

; ekkor a kúpszelet, minthogy még

Δ \neq 0

hiperbola. Ha azonban

m = 0

, akkor az

\begin{matrix} (y - 3) (4 x - 3 y) = 0, \end{matrix}

ha pedig

m = \pm \infty

, akkor az

\begin{matrix} (x - 8) (3 x - 2 y) = 0 \end{matrix}

egyenespárral van dolgunk.
Ha

m = 1

, akkor

δ = 0

és

Δ = 0

, akkor párhuzamos egyenesek párját kapjuk:

\begin{matrix} (x - y) (x - y + 1) = 0 \end{matrix}

m = 4

esetben

δ = 0,

Δ \neq 0

, parabolát kapunk, melynek egyenlete:

\begin{matrix} {(2 x - y)}^{2} - 8 x + 5 y = 0. \end{matrix}

Végül, ha

1 < m < 4

, akkor

δ > 0

és

A Δ < 0;

ezen esetekben ellipszissel van dolgunk.

Alpár László (Izr. rg. VIII. o. Bp.)