Feladat:	787. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. ,  Bordás S. ,  Csernussi E. ,  Deutsch E. ,  Emődi M. ,  Fröhlich Károly ,  Gajzágó E. ,  Gál I. ,  Giesser Gy. ,  Gyarmati B. ,  Jahoda A. ,  Kepes J. ,  Kolma I. ,  Lehel P. ,  Manner L. ,  Mérei L. ,  Róth Edit ,  Róth Sz. ,  Ruhmann M. ,  Sohr Anna ,  Stolcz T. ,  Szabó I. ,  v. Bánföldy A. ,  Vezér Gy. ,  Weiszfeld E.
Füzet:	1932/május, 264 - 266. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek egybevágósága, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1932/március: 787. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.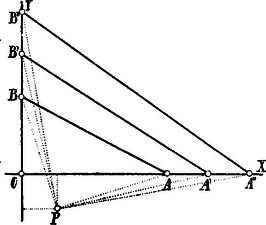   I. Megoldás. Legyen $AA\text{'}=BB\text{'}=u$. Az $A\text{'}B\text{'}$ egyenes egyenlete: $\begin{array}{c}{\displaystyle \frac{x}{a+u}+\frac{y}{b+u}=1.}\end{array}$ Irányhatározója $-\frac{b+u}{a+u}$. A reá merőleges egyenesé: $\frac{a+u}{b+u}$. Minthogy az $A\text{'}B\text{'}$ távolság felező pontjának koordinátái: $\frac{a+u}{2}$, $\frac{b+u}{2}$, azért ezen ponton átmenő és az $A\text{'}B\text{'}$-re merőleges egyenes egyenlete: $\begin{array}{c}{\displaystyle y-\frac{b+u}{2}=\frac{a+u}{b+u}\left(x-\frac{a+u}{2}\right)\mathrm{,}}\end{array}$ ill. $\begin{array}{c}{\displaystyle \left(2by-2ax+a^2-b^2\right)+2u\left(y-x+a-b\right)=0.}\end{array}$ (1) Ezen egyenes az $u$ bármely értéke mellett keresztülmegy a $\begin{array}{c}{\displaystyle 2by-2ax+a^2-b^2=0}\end{array}$ (2) és $\begin{array}{c}{\displaystyle y-x+a-b=0}\end{array}$ (3) egyenesek közös $P$ pontján, amelynek koordinátái $\begin{array}{c}{\displaystyle x=\frac{a-b}{2}\mathrm{,}y=\frac{b-a}{2}\mathrm{.}}\end{array}$ Fröhlich Károly (Mátyás Király rg. VIII. o. Bp. II.)   Jegyzet. Ha $u=-b$, akkor $P$ pont az $y=\frac{a-b}{2}$ egyenesen fekszik. Ha $u=-a$, akkor a $P$ pont az $x=\frac{b-a}{2}$ egyenesen fekszik. A (2) egyenlet az $u=0$ esetnek megfelelő, tehát az $AB$-t felező merőleges egyenlete. A (3) az $u=\infty$ értékhez tartozó merőleges egyenlete. Világossá válik ez akkor, ha az (1) egyenletet előbb az $\begin{array}{c}{\displaystyle \frac{1}{2u}\left(2by-2ax+a^2-b^2\right)+\left(y-x+a-b\right)=0}\end{array}$ alakban írjuk. Az (1) egyenlet a $P$ ponton átmenti sugársor egyenlete.   II. Megoldás. Az $AB$ és $A\text{'}B\text{'}$ távolságokat merőlegesen felező egyenesek metszéspontja legyen $P$. Kimutatjuk, hogy a $P$ ponton keresztülmegy az $A\text{'}\text{'}B\text{'}\text{'}$ távolságot merőlegesen felező egyenes is, ha $AA\text{'}\text{'}=BB\text{'}\text{'}$. Ugyanis $PAA\text{'}▵\cong PBB\text{'}▵$ (mert: $PA=PB$, $PA\text{'}=PB\text{'}$, és $AA\text{'}=BB\text{'}$). Ezért $PAA\text{'}\sphericalangle =PBB\text{'}\sphericalangle$. Így azonban $PAA\text{'}\text{'}▵\cong PBB\text{'}\text{'}▵$ (mert: $PA=PB$, $AA\text{'}\text{'}=BB\text{'}\text{'}\sphericalangle$ és $PAA\text{'}\text{'}\sphericalangle =PBB\text{'}\text{'}\sphericalangle$). Ebből következik, hogy $PA\text{'}\text{'}=PB\text{'}\text{'}$, azaz a $P$ ponton keresztül megy az $A\text{'}\text{'}B\text{'}\text{'}$ felezőmerőlegese is.   Sohr Anna (izr. leányg. VII. o. Bp.)