Kezdőlap


Feladat:	766. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Baneth L. , Bihari I. , Blazsek I. , Bordás S. , Busztin Anna , Ehrenfeld Gy. , Eisenberg A. , Emődi M. , Erdős Gy. , Gajzágó E. , Geba I. , Giesser Gy. , Koma I. , Kovács K. , Lehel P. , Lukács O. , Megyery E. , Mérei L. , Pintér Gy. , Prém L. , Réffy K. , Rimóczy G. , Singer G. , Singer I. , Sohr Anna , Szabó J. , Székely I. , Tarnóczy T. , Vona Gy. , Weiszfeld E.
Füzet:	1932/március, 192 - 194. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Irracionális egyenletek, Paraméteres egyenletek, Hiperbola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1932/január: 766. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Minthogy az egyenletben szereplő négyzetgyök pozitív számot, határesetben zérust jelent, az egyenletet csak $x \geq 1$ értékek elégíthetik ki. Négyzetre emelés és rendezés után

\begin{matrix} f (x) \equiv 4 x^{2} + 4 x - (k + 1) = 0 \end{matrix}

(1)

egyenlethez jutunk. Ennek valósak a gyökei, ha

\begin{matrix} 16 + 16 (k + 1) \geq 0, vagy k \geq - 2. \end{matrix}

(2)

Minthogy a gyökök félösszege:

- \frac{4}{8} = - \frac{1}{2}

, az egyik gyök mindig

< - \frac{1}{2}

, a másik

> - \frac{1}{2}

: Az előbbi tehát nem jöhet tekintetbe; az utóbbi pedig csak akkor, ha

\begin{matrix} f (1) = 7 - k \leq 0, azaz k \geq 7. \end{matrix}

(3)

Eszerint az adott egyenletnek a

k \geq 7

értékekkel van egy és csakis egy megoldása, mégpedig

\begin{matrix} x = \frac{- 1 + \sqrt[]{2 + k}}{2} . \end{matrix}

2^{\circ}

. Az egyenlet megoldásának geometriai értelme: keresnünk kell az

\begin{matrix} y = \sqrt[]{5 x^{2} + 2 x - k} görbe & (4) \\ és y = x - 1 egyenes . & (5) \end{matrix}

közös pontjait, figyelemmel arra, hogy a (4) függvény értékkészletéből a negatív értékeket kizártuk.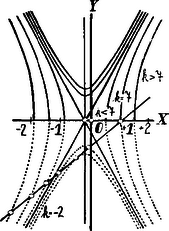

y^{2} = 5 x^{2} + 2 x - k

hiperbola egyenlete; azonban az adott egyenlet szempontjából a hiperbolának az

X

-tengely feletti része jöhet tekintetbe. Ha a jobboldal discriminánsa:

4 + 20 k < 0

, azaz

k < - \frac{1}{5}

, a jobboldal

x

minden értékénél pozitív; minden

x

értékhez a görbének az

X

-tengelyre nézve szimmetrikus pontjai tartoznak. Az

X

-tengely a hiperbola képzetes tengelye; a hiperbola valós tengelye az

x = - \frac{1}{5}

egyenes. Középpontjának koordinátái

x = - \frac{1}{5}

y = 0

. Aszimptotái az

y^{2} - 5 x^{2} = 0

egyenespár egyeneseivel párhuzamosak. Mindezen hiperbolák közül az

y = x - 1

egyenes azokat nem metszi, amelyekre

k < - 2

.
A

k = - 2

értékhez tartozó hiperbolát az

y = x - 1

egyenes érinti, de nem az

X

-tengely feletti ágát.
Ha

- 2 < k < - \frac{1}{5}

, a hiperbolát az

y = x - 1

egyenes az

X

-tengely alatt metszi (két pontban).

k = - \frac{1}{5}

értékkel a hiperbola egyenespárrá fajul:

y^{2} = 5 {(x + \frac{1}{5})}^{2}

. Ezen egyenespárnak és az (5) egyenesnek közös pontjai az

X

-tengely alatt vannak.
Ha

k > - \frac{1}{5}

, akkor oly hiperbolákkal van dolgunk, amelyeknek valós tengelyük az

X

-tengely; a görbe két pontban metszi az

X

-tengelyt és ez a görbe egyik szimmetria tengelye. E hiperbolák középpontja most is az

(x = - \frac{1}{5}, y = 0)

pont; képzetes tengelyük most az

x = - \frac{1}{5}

egyenes; aszimptotáik most is ugyanazok, mint az előbb. Mindaddig, amíg

- \frac{1}{5} < k < + 7

, a hiperbola és az (5) egyenes közös pontjai az

X

-tengely alatt vannak.

k = 7

esetben a hiperbola és az (5) egyenes egyik közös pontja

x = 1

y = 0

; a másik közös pontjuk az

X

-tengely alatt van.

k < 7

értékekkel a hiperbola és az (5) egyenes egyik közös pontja az

X

-tengely felett van (

x > 1

y > 0

), a másik közös pontjuk az

X

tengely alatt van. Az (1) egyenlet gyökei a két közös pont abscissáit szolgáltatják, de ezek közül csak az egyik felel meg az adott irracionális egyenletnek.