Kezdőlap


Feladat:	757. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Baneth L. , Braun J. , Ehrenfeld Gy. , Emődi M. , Farkas V. , Gajzágó E. , Geba I. , Gyarmati B. , Hegedüs T. , Lénárt J. , Mérei L. , Mitnyán L. , Papp Zs. , Pintér György , Róna I. , Scholcz G. , Singer G. (IV. o. t.) , Szabó I. , Székely I. , Varga Á. , Weiszfeld E.
Füzet:	1932/február, 165 - 166. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Beírt kör, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1931/december: 757. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B C_{▵}$ a feltételeknek megfelelő háromszög; az $A$ csúcsból vont magasság talppontja a $B C$ oldalon $A_{1}$ , a beírt kör középpontja $O$ , e kör érintési pontja a $B C$ oldalon $A_{2}$ , tehát $O A_{2} = r$ és $O$ vetülete az $A A_{1} = m_{a}$ magasságon 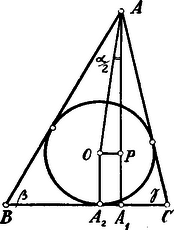$P$ .

A O P_{▵}

adatainkból megszerkeszthető. Ugyanis

\begin{matrix} A P = A A_{1} - P A_{1} = A A_{1} - O A_{2} = m_{a} - r; \\ O A P ∢ = B A A_{1} ∢ - B A O ∢ = 90^{\circ} - β - \frac{α}{2} = \frac{α + β + γ}{2} - β - \frac{α}{2} = \frac{γ - β}{2} = \frac{δ}{2} . \end{matrix}

Eszerint az

A O P

derékszögű háromszögnek egyik befogója és egyik hegyesszöge az adatokból megszerkeszthető, tehát

A O P_{▵}

is.
Az

A O P_{▵}

-et megszerkesztve,

O

-ból

r

sugárral kört rajzolunk, amelyhez

A

pontból érintőket szerkesztünk; az

A P

-t

P A_{1} = r

hosszúsággal megnövelve, jutunk az

A_{2}

-höz, amelyből az

O

körhöz az

A A_{1}

-re merőleges érintőt húzunk. Ezen érintő az előbbi kettővel meghatározza az

A B C_{▵}

-et. (1. megoldás!)
A szerkesztés lehetséges, ha

\frac{δ}{2} < 90^{\circ}

, tehát

δ < 180^{\circ}

; továbbá, ha

A

O

pontból

r

sugárral rajzolt körön kívül van és

B A P ∢ < 90^{\circ}

. (Az

A B

érintő ne legyen párhuzamos

O P

-vel!). Tehát kell, hogy

\begin{matrix} O A > r és A P > r . \end{matrix}

Azonban,

A P > r

feltétel kielégítése maga után vonja az

O A > r

feltétel kielégítését is. Az

A P = m_{a} - r > r

azt jelenti, hogy

m_{a} > 2 r

legyen.

Pintér György (Kemény Zsigmond r. VI. o. Bp. VI.)