Kezdőlap


Feladat:	755. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Alpár L. , Bordás Sándor , Busztin Anna , Emődi M. , Farkas Vilmos , Gajzágó E. , Geba I. , Giessner Gy. , Gyarmati B. , Hegedüs T. , Nánási Gy. , Papp Zs. , Parti S. , Pintér Gy. , Varga Á. , Weiszfeld E.
Füzet:	1932/február, 163 - 164. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Egyenes, Párhuzamos szelők tétele, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1931/december: 755. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Vizsgáljuk először a háromszögeket, ha szilárd a $b + c = B D = s$ távolság. A feltételeknek megfelelő bármely háromszöget úgy kapunk, ha a $B D = s$ távolságra a $D$ végpontjában felmérjük az $\frac{α}{2}$ szöget; ennek egyik szára 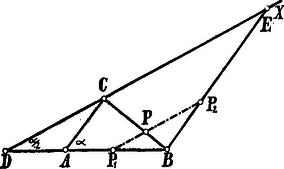$D B$ , a másik $D X$ .

Minthogy a háromszög harmadik oldala

B C = a < b + c

, a

B

pontból

s

sugárral rajzoljunk kört, amely a

D X

-et (a

D

-n kívül még) az

E

pontban metszi. A

D X

egyenes

D E

darabjának bármelyik pontja lehet a háromszög egyik csúcsa,

C

. A

D C

távolság felezőpontjában

D C

-re állított merőleges

B D

-t a háromszög harmadik csúcsában az

A

-ban metszi. Az így nyert

A B C_{▵}

megfelel a feltételeknek, mert

\begin{matrix} B A + A C = B A + A D = s \end{matrix}

és

\begin{matrix} B A C ∢ = A D C ∢ + A C D ∢ = \frac{α}{2} + \frac{α}{2} = α . \end{matrix}

Ha már most a

B

pontot a

D E

szakasz bármely

C

pontjával összekötjük és ezen

B C

-n kijelöljük a

P

pontot a

B P : P C = λ

feltételnek megfelelőleg, a

P

pontok mértani helye a

D E

-vel párhuzamos egyenes darabja lesz (

B D

és

B E

között):

P_{1} P_{2}

Farkas Vilmos (Révai Miklós r. VII. o. Győr.)

b) Vegyük most az

\hat{X A Y} = α

szöget szilárdnak, melynek

A X

szárán mozoghat a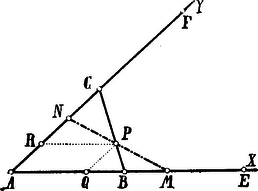

B

pont az

E

-ig, ha

A E = s

és

A Y

szárán a

C

pont az

F

-ig, ha

A F = s

Tegyük fel, hogy a

A B C_{▵}

egy, a feltételnek megfelelő háromszög, azaz

A B + A C = s

és a

B C

-n felvett

P

pontra nézve

B P : P C = λ

. Tekintsük

A X

és

A Y

egyeneseket egy ferdeszögű koordinátarendszer tengelyeinek, amelyekkel a

P

pontból párhuzamosakat vonunk, tehát

P Q = y

és

A Q = x

P

koordinátái). Minthogy

P R ∥ A X

és

P R = A Q = x

R A = P Q = y

, a következő aránypárokat írhatjuk:

\begin{matrix} R P : P C = B Q : A Q, \end{matrix}

vagyis

\begin{matrix} λ = \frac{c - x}{x} és innen c = x (1 + λ), \end{matrix}

és

\begin{matrix} B P : P C = P Q : C R, \end{matrix}

vagyis

\begin{matrix} λ = \frac{y}{b - y} és innen b = y \frac{1 + λ}{λ} . \end{matrix}

Minthogy

b + c = s

, a

P

pont koordinátái az

\begin{matrix} (1 + λ) x + y \frac{1 + λ}{λ} = s ill. \frac{x}{\frac{s}{1 + λ}} + \frac{y}{\frac{λ s}{1 + λ}} = 1 \end{matrix}

egyenletet elégítik ki. A

P

pont eszerint ezen egyenlet által meghatározott egyenesen fekszik, de ennek csak az

A X

és

A Y

egyenesek közé eső részét írja le.
Ha pl.

λ = 1 : 3

, akkor a

P

pont mértani helye

M N

, mégpedig

\begin{matrix} A M = \frac{s}{1 + \frac{1}{3}} = \frac{3 s}{4} és A N = \frac{\frac{s}{3}}{1 + \frac{1}{3}} = \frac{s}{4} . \end{matrix}

Bordás Sándor (Klauzál Gábor rg. VII. o. Szeged.)